题目内容
【题目】将两个等边△ABC和△DEF(DE>AB)如图所示摆放,点D是BC上的一点(除B、C点外).把△DEF绕顶点D顺时针旋转一定的角度,使得边DE、DF与△ABC的边(除BC边外)分别相交于点M、N.
(1)∠BMD和∠CDN相等吗?
(2)画出使∠BMD和∠CDN相等的所有情况的图形.
(3)在(2)题中任选一种图形说明∠BMD和∠CDN相等的理由.
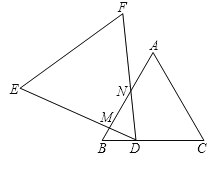
【答案】(1)相等;(2)有四种情况,答案见解析;(3)答案见解析.
【解析】
(1)根据三角形内角和定理以及外角性质,在△BMD中利用三角形内角和定理,再根据∠MDC是△BMD的外角即可得出;
(2)根据(1)中三角形和定理和外角性质分类画出图形,即可解答;
(3)根据三角形的内角和定理和平角的定义,即可得出.
(1)相等.
(2)有四种情况,如下:

(3)选④证明:
∵△ABC和△DEF均为等边三角形,∴∠B=∠EDF=60°,∴∠ADB+∠BMD+∠B=180°,∠EDF+∠ADB+∠CDN=180°,∴∠BMD=∠CDN.

练习册系列答案
相关题目