题目内容
【题目】新定义:我们把只有一组对角是直角的四边形叫做准矩形.
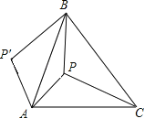
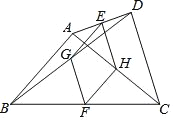
(1)图①、图②均为3×3的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.线段AB、BC的端点均在格点上,在图①、图②中各画一个准矩形ABCD,要求:准矩形ABCD的顶点D在格点上,且两个准矩形不全等.
(2)如图③,正方形ABCD的边长为4,准矩形ABMN的顶点M、N分别在正方形ABCD的边上.若准矩形ABMN的一条对角线长为5,直接写出此时该准矩形的面积
【答案】
(1)解:如图①,图②所示.

(2)解:如图③,

在正方形ABCD中,∠ABC=∠D=90°,
∵∠ANM=90°,
∴∠DAN=∠CNM(同角的余角相等),
∴△ADN∽△NCM,
∴ ![]() =
= ![]() .
.
①连接AM,
当AM=5时,在直角△ABM中,AB=4,∠ABC=90,AM=5,则由勾股定理得到:BM= ![]() =
= ![]() =3,
=3,
所以CM=4﹣3=1.
所以 ![]() =
= ![]() ,
,
则DNNC=4.
又DN+NC=4,
∴DN=NC=2,
∴S准矩形ABMN=S正方形ABCD﹣S△ADN﹣S△NCM=4×4﹣ ![]() ×4×2﹣
×4×2﹣ ![]() ×2×1=11;
×2×1=11;
②连接BN,
当BN=5时,在直角△BCN中,AB=4,∠ABC=90,BN=5,则由勾股定理得到:CN= ![]() =
= ![]() =3,
=3,
所以DN=4﹣3=1.
所以 ![]() =
= ![]() ,
,
∴CM= ![]() ,
,
∴S准矩形ABMN=S正方形ABCD﹣S△ADN﹣S△NCM=4×4﹣ ![]() ×4×1﹣
×4×1﹣ ![]() ×3×
×3× ![]() =
= ![]() ;
;
综上所述,此时该准矩形的面积是11或= ![]() .
.
【解析】(1)以AC为直径画圆与格点相交的D点都符合题意;(2)对角线长为5,须分类讨论,AM=5或BN=5,利用相似三角形和勾股定理,可求出准矩形的面积.
【考点精析】关于本题考查的正方形的性质和相似三角形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;对应角相等,对应边成比例的两个三角形叫做相似三角形才能得出正确答案.

【题目】某电器商城销售![]() 、
、![]() 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为![]() 元、
元、![]() 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:
销售时段 | 销售型号 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 、
、![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商城准备用不多于![]() 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共![]() 台,求
台,求![]() 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在(2)的条件下商城销售完这![]() 台电风能否实现利润超过
台电风能否实现利润超过![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.