题目内容
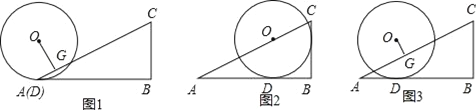
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
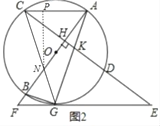
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

【答案】(1)证明见解析;(2)证明见解析;(3)CN=![]() .
.
【解析】试题分析:
(1)连接OG,则由已知易得∠OGE=∠AHK=90°,由OG=OA可得∠AGO=∠OAG,从而可得∠KGE=∠AKH=∠EKG,这样即可得到KE=GE;
(2)设∠FGB=α,由AB是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE可得∠EKG=90°-α,这样在△GKE中可得∠E=2α,由∠FGB=![]() ∠ACH可得∠ACH=2α,这样可得∠E=∠ACH,由此即可得到CA∥EF;
∠ACH可得∠ACH=2α,这样可得∠E=∠ACH,由此即可得到CA∥EF;
(3)如下图2,作NP⊥AC于P,
由(2)可知∠ACH=∠E,由此可得sinE=sin∠ACH=![]() ,设AH=3a,可得AC=5a,CH=4a,则tan∠CAH=
,设AH=3a,可得AC=5a,CH=4a,则tan∠CAH=![]() ,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC,从而可得CK=AC=5a,由此可得HK=a,tan∠AKH=
,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC,从而可得CK=AC=5a,由此可得HK=a,tan∠AKH=![]() ,AK=
,AK=![]() a,结合AK=
a,结合AK=![]() 可得a=1,则AC=5;在四边形BGKH中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG可得∠ACG=∠AKH,
可得a=1,则AC=5;在四边形BGKH中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG可得∠ACG=∠AKH,
在Rt△APN中,由tan∠CAH=![]() ,可设PN=12b,AP=9b,由tan∠ACG=
,可设PN=12b,AP=9b,由tan∠ACG=![]() tan∠AKH=3可得CP=4b,由此可得AC=AP+CP=
tan∠AKH=3可得CP=4b,由此可得AC=AP+CP=![]() =5,则可得b=
=5,则可得b=![]() ,由此即可在Rt△CPN中由勾股定理解出CN的长.
,由此即可在Rt△CPN中由勾股定理解出CN的长.
试题解析:
(1)如图1,连接OG.
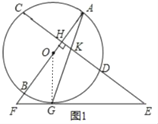
∵EF切⊙O于G,
∴OG⊥EF,
∴∠AGO+∠AGE=90°,
∵CD⊥AB于H,
∴∠AHD=90°,
∴∠OAG=∠AKH=90°,
∵OA=OG,
∴∠AGO=∠OAG,
∴∠AGE=∠AKH,
∵∠EKG=∠AKH,
∴∠EKG=∠AGE,
∴KE=GE.
(2)设∠FGB=α,
∵AB是直径,
∴∠AGB=90°,
∴∠AGE=∠EKG=90°﹣α,
∴∠E=180°﹣∠AGE﹣∠EKG=2α,
∵∠FGB=![]() ∠ACH,
∠ACH,
∴∠ACH=2α,
∴∠ACH=∠E,
∴CA∥FE.
(3)作NP⊥AC于P.
∵∠ACH=∠E,
∴sin∠E=sin∠ACH=![]() ,设AH=3a,AC=5a,
,设AH=3a,AC=5a,
则CH=![]() ,tan∠CAH=
,tan∠CAH=![]() ,
,
∵CA∥FE,
∴∠CAK=∠AGE,
∵∠AGE=∠AKH,
∴∠CAK=∠AKH,
∴AC=CK=5a,HK=CK﹣CH=4a,tan∠AKH=![]() =3,AK=
=3,AK= ![]() ,
,
∵AK=![]() ,
,
∴![]() ,
,
∴a=1.AC=5,
∵∠BHD=∠AGB=90°,
∴∠BHD+∠AGB=180°,
在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,
∴∠ABG+∠HKG=180°,
∵∠AKH+∠HKG=180°,
∴∠AKH=∠ABG,
∵∠ACN=∠ABG,
∴∠AKH=∠ACN,
∴tan∠AKH=tan∠ACN=3,
∵NP⊥AC于P,
∴∠APN=∠CPN=90°,
在Rt△APN中,tan∠CAH=![]() ,设PN=12b,则AP=9b,
,设PN=12b,则AP=9b,
在Rt△CPN中,tan∠ACN=![]() =3,
=3,
∴CP=4b,
∴AC=AP+CP=13b,
∵AC=5,
∴13b=5,
∴b=![]() ,
,
∴CN=![]() =
= ![]() =
=![]() .
.

 智趣暑假温故知新系列答案
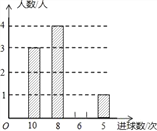
智趣暑假温故知新系列答案【题目】某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中选一名学生参加校动会投篮比赛,投进10球的成员被选中的概率为多少?