题目内容
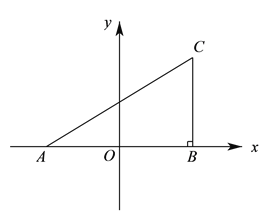
【题目】如图，过y轴上任意一点p，作x轴的平行线，分别与反比例函数y=－
和y=
的图象交于A点和B点．若C为x轴上任意一点，连接AC、BC，则△ABC的面积为 ．
【答案】3．
【解析】
试题分析：先设P（0，b），由直线AB∥x轴，则A，B两点的纵坐标都为b，而A，B分别在反比例函数y=-
和y=
的图象上，可得到A点坐标为（-
，b），B点坐标为（
，b），从而求出AB的长，然后根据三角形的面积公式计算即可．
试题解析：设P（0，b），
∵直线AB∥x轴，
∴A，B两点的纵坐标都为b，而点A在反比例函数y=-的图象上，
∴当y=b，x=-，即A点坐标为（-，b），
又∵点B在反比例函数y=的图象上，
∴当y=b，x=，即B点坐标为（，b），
∴AB=-（-）=
，
∴S△ABC=
ABOP=b=3．
练习册系列答案
相关题目
【题目】某手机销售商分别以每部进价分别为800元、670元的A、B两种型号的手机，下表是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 6台 | 7650元 |
第二周 | 4台 | 10台 | 11800元 |
（进价、售价均保持不变，利润=销售收入﹣进货成本）
（1)求A、B两种型号的手机的销售单价；
（2)若手机销售商准备再采购这两种型号的手机共30台，且利润不低于4000元，求A种型号的手机至少要采购多少台？
