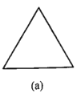
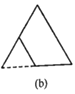
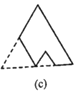
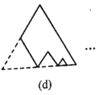
题目内容
【题目】如图所示,![]() 绕点A旋转
绕点A旋转![]() 得到
得到![]() ,
,
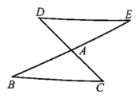
(1)则DE与BC的位置关系是_________,数量关系是_________;
(2)若![]() ,则
,则![]() _________;
_________;
(3)若![]() ,
,![]() ,
,![]() 的周长为偶数,则AE的长为_________;
的周长为偶数,则AE的长为_________;
【答案】(1)![]() ;
;![]() ;(2)24;(3)4.
;(2)24;(3)4.
【解析】
(1)根据旋转的性质可得,DE=BC,∠E=∠B,然后根据内错角相等,两直线平行即可得出结论;
(2)根据旋转的性质可得△AED≌△ABC,从而得出结论;
(3)根据旋转的性质可得AD=AC=2,ED=BC=4,然后根据三角形的周长和三边关系即可求出AE的长.
解:(1)由旋转的性质可得:DE=BC,∠E=∠B
∴![]()
故答案为:![]() ;
;![]() .
.
(2)由旋转的性质可得△AED≌△ABC,
∴![]()
![]()
故答案为:24.
(3)由旋转的性质可得AD=AC=2,ED=BC=4,
在△ADE中,ED -AD<AE<ED+AD
即2<AE<6
∵![]() 的周长为偶数,AD、ED均为偶数
的周长为偶数,AD、ED均为偶数
∴AE也为偶数
∴AE=4
故答案为:4.

练习册系列答案
相关题目