题目内容
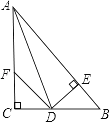
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用HL证明RT△CDF≌RT△EDB即可得出CF=EB;
(2)利用HL证明RT△ADE≌RT△ADC即可得出AC=AE,再由AB=AE+EB=AF+CF+EB进行等量代换即可.
(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,
![]() ,
,
∴Rt△CDF≌Rt△EDB(HL)
∴CF=EB
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,![]() ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.

练习册系列答案
相关题目
【题目】有20筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?