题目内容
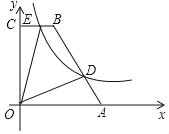
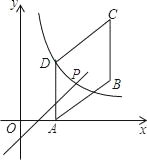
【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=![]() (x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
①反比例函数的解析式是y1=![]() ;
;
②一次函数y2=kx+3﹣3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3﹣3k的图象经过点C,当x>2![]() 时,y1<y2;
时,y1<y2;
④对于一次函数y2=kx+3﹣3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是0<a<3.
其中正确的是( )
A. ①③ B. ②③ C. ②④ D. ③④
【答案】D
【解析】分析:①根据平行四边形的性质求D点的坐标;(2)把x=6代入y2=kx+3﹣3k中,看函数值是否为6;③把点C的坐标代入y2=kx+3﹣3k,求得一次函数的解析,由一次函数的解析式和反比例函数的解析组成的方程组可求得它们的交点坐标,结合函数图象判断;④一次函数过定点(3,3),确定x=3时的函数值即可.
详解:①∵四边形ABCD是平行四边形,∴AD=BC,
∵B(6,2),C(6,6),∴BC⊥x轴,AD=BC=4,而A点坐标为(2,0),
∴点D的坐标为(2,4),
∵反比例函数y1=![]() (x>0)的函数图象经过点D(2,4),
(x>0)的函数图象经过点D(2,4),
∴4=![]() ,∴m=8,
,∴m=8,
∴反比例函数的解析式为y=![]() ,①不正确;
,①不正确;
②当x=6时,y=kx+3﹣3k=6k+3﹣3k=3k+3≠6,
∴一次函数y=kx+3﹣3k(k≠0)的图象不一定过点C,②不正确;
③∵一次函数y2=kx+3﹣3k的图象经过点C,
∴6=6k+3﹣3k,解得:k=1.
∴y2=x.
联立![]() ,解得:
,解得:![]() 或
或![]() (舍去).
(舍去).
结合函数图象即可得出:
当x>![]() 时,y1<y2,③成立;
时,y1<y2,③成立;
④∵一次函数y2=kx+3﹣3k(k≠0),y随x的增大而增大,
∴k>0,∴交点P在第一象限.
将x=3代入到反比例函数y=![]() 中,得:y=
中,得:y=![]() .
.
∵因为y2-3=k(x﹣3),当x=3时,y2=3,
∴一次函数y2=kx+3﹣3k(k≠0)恒过点(3,3),点(3,![]() )在(3,3)的下方,
)在(3,3)的下方,
即点P应该在点(3,![]() )的左方,∴点P横坐标a的取值范围是a<3.
)的左方,∴点P横坐标a的取值范围是a<3.
即④正确.
综上可知:③④正确,
故选D.

 阅读快车系列答案
阅读快车系列答案【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如下表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们20%、10%、30%和40%的权重,请分别计算两名选手的最终成绩,从他们的这一成绩看,应选派谁.