Question

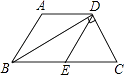
【题目】如图所示，在梯形ABCD中，AD∥BC，∠BDC=90°，E为BC上一点，∠BDE=∠DBC．
（1）求证：DE=EC；
（2）若AD= BC，试判断四边形ABED的形状，并说明理由．

Answer 1

【答案】
（1）证明：∵∠BDC=90°，∠BDE=∠DBC，

∴∠EDC=∠BDC﹣∠BDE=90°﹣∠BDE，

又∵∠C=90°﹣∠DBC，

∴∠EDC=∠C，

∴DE=EC；

（2）若AD= BC，则四边形ABED是菱形．

证明：∵∠BDE=∠DBC．

∴BE=DE，

∵DE=EC，

∴DE=BE=EC= BC，

∵AD= BC，

∴AD=BE，

∵AD∥BC，

∴四边形ABED是平行四边形，

∵BE=DE，

∴ABED是菱形．

【解析】（1）由∠BDC=90°，∠BDE=∠DBC，利用等角的余角相等，即可得∠EDC=∠C，又由等角对等边，即可证得DE=EC；（2）易证得AD=BE，AD∥BC，即可得四边形ABED是平行四边形，又由BE=DE，即可得四边形ABED是菱形．
【考点精析】掌握菱形的判定方法和梯形的定义是解答本题的根本，需要知道任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形；一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形．