��Ŀ����
����Ŀ����ֱ֪��y=kx+3��k��0���ֱ�x�ᡢy����A��B���㣬�߶�OA����һ����P��ԭ��O���A�˶����ٶ�Ϊÿ��1����λ���ȣ�����P��x��Ĵ��߽�ֱ��AB�ڵ�C�����˶�ʱ��Ϊt�룮
��1����k=��1ʱ���߶�OA������һ����Q�ɵ�A���O�˶��������P����ͬ�ٶ�ͬʱ����������P�����Aʱ����ͬʱֹͣ�˶�����ͼ1����
��ֱ��д��t=1��ʱC��Q��������ꣻ
������Q��C��AΪ��������������AOB���ƣ���t��ֵ��
��2���� ![]() ʱ������CΪ�����������y=��x+m��2+n��ֱ��AB����һ����ΪD����ͼ2����
ʱ������CΪ�����������y=��x+m��2+n��ֱ��AB����һ����ΪD����ͼ2����
����CD�ij���
�����COD��OC���ϵĸ�Ϊh����tΪ��ֵʱ��h��ֵ���
���𰸡�
��1��
�⣺��C��1��2����Q��2��0��
��������ã�P��t��0����C��t����t+3����Q��3��t��0����
������������ۣ�
����һ������AQC�ס�AOBʱ����AQC=��AOB=90�㣬
��CQ��OA��
��CP��OA��
���P���Q�غϣ�OQ=OP��
��3��t=t��
��t=1.5��
���ζ�������ACQ�ס�AOBʱ����ACQ=��AOB=90�㣬
��OA=OB=3��
���AOB�ǵ���ֱ�������Σ�
���ACQҲ�ǵ���ֱ�������Σ�
��CP��OA��
��AQ=2CP��
��t=2����t+3����
��t=2��
������������t��ֵ��1.5���2��
��2��
��������ã�C��t���� ![]() ����
����
����CΪ����������߽���ʽ��y= ![]() ��
��
�� ![]() ��
��
����x��t��2+ ![]() ��x��t��=0��
��x��t��=0��
�ࣨx��t����x��t+ ![]() ��=0��
��=0��
��� ![]() ��
��
����D��DE��CP�ڵ�E�����DEC=��AOB=90�㣬
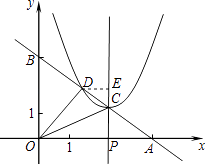
��DE��OA��
���EDC=��OAB��
���DEC�ס�AOB��
�� ![]() ��
��
��AO=4��AB=5��DE= ![]() ��
��
��CD= ![]() ��
��
�ڡ� ![]() ��CD���ϵĸ�=
��CD���ϵĸ�= ![]() ��
��
�� ![]() ��
��
��S��CODΪ��ֵ��
ҪʹOC���ϵĸ�h��ֵ���ֻҪOC��̣���Ϊ��OC��ABʱOC��̣�
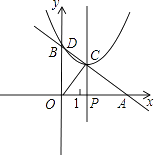
��ʱOC�ij�Ϊ ![]() ����BCO=90�㣬
����BCO=90�㣬
�ߡ�AOB=90�㣬
���COP=90�㩁��BOC=��OBA��
�֡�CP��OA��
��Rt��PCO��Rt��OAB��
�� ![]() ��OP=
��OP= ![]() ��
��
��t= ![]() ��
��
�൱tΪ ![]() ��ʱ��h��ֵ���
��ʱ��h��ֵ���
����������1����������ɵã���������õ�����t�����꣮�����������ν�𣬴Ӷ��õ��𰸣���2�����Ե�CΪ����������ߣ���ù���t�ĸ������ɹ���D��DE��CP�ڵ�E�����DEC=��AOB=90�㣬���ɡ�DEC�ס�AOB�Ӷ���ã��������������COD�����Ϊ��ֵ������Rt��PCO��Rt��OAB�����߶α�����tΪ ![]() ʱ��h���
ʱ��h���

 53������ϵ�д�
53������ϵ�д�




