Question

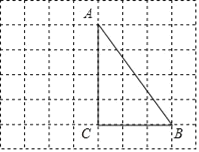
【题目】如图，在等腰直角△ABC中，∠C＝90°，AB＝10，点F是AB的中点，点D、E分别在AC、BC边上运动，且始终保持DF⊥EF，则△CDE面积的最大值为__．

Answer 1

【答案】

【解析】

连接CF，根据全等三角形的判定定理可判定△ADF≌△CEF，设AD＝x，△CDE的面积为y，则CE＝x，∠C＝90°，列出y关于x的二次函数，利用最值点即可得到答案．

解：如图所示，连接CF，

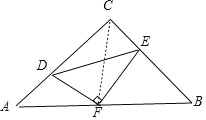
∵等腰直角△ABC中，∠C＝90°，AB＝10，点F是AB的中点，

∴CF＝AF，∠A＝∠FCE，AC＝BC＝10×＝5，

又∵∠DFC+∠CFE＝90°，∠AFD+∠CFD＝90°，

∴∠AFD＝∠CFE，

∴△ADF≌△CEF（ASA），

设AD＝x（0＜x＜5），△CDE的面积为y，则CE＝x，CD＝5﹣x，∠C＝90°，

∴y＝x（5﹣x）＝﹣+，

即△CDE面积的最大值为，

故答案为：．