Question

【题目】直线y=﹣x+c与x轴交于点A（4，0），与y轴交于点B，抛物线y=﹣x2+bx+c经过A、B两点．

(1)求抛物线表达式；

(2)点P为抛物线上的一个动点，过点P作垂直于x轴的直线分别交x轴和直线AB于M、N两点，若P、M、N三点中恰有一点是其他两点所连线段的中点（三点重合除外），请求出此时点P的坐标．

Answer 1

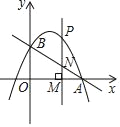
【答案】(1)抛物线解析式为y=﹣+2；(2)满足条件的P点坐标为（﹣，）或（﹣2，﹣3）或（1，3）．

【解析】

（1）先把A点坐标代入y=-x+c中求出c=2，从而得到一次函数解析式为y=-x+2，然后把A点坐标代入y=-x2+bx+2中求出b即可得到抛物线解析式；
（2）设P（x，-x2+x+2），则N（x，-x+2），M（x，0），讨论：当x＞4时，MN=MP，则-（-x+2）=-x+2-（-x2+x+2）；当0＜x＜4时，PN=MN，则-x2+x+2-（-x+2）=-x+2；当-1＜x＜0时，NP=PM，-x+2-（-x2+x+2）=-x2+x+2；当x＜-1时，NM=PM，-x+2=-（-x2+x+2），然后分别解方程得到对应P点坐标．

(1)把A（4，0）代入y=﹣x+c得﹣2+c=0，解得c=2，

∴一次函数解析式为y=﹣x+2，

当x=0时，y=﹣x+2=2，则B（0，2），

把A（4，0）代入y=﹣+bx+2得﹣8+4b+2=0，解得b=，

∴抛物线解析式为y=﹣+x+2；

(2)设P（x，﹣+x+2，则N（x，﹣x+2），M（x，0），

当x＞4时，MN=MP，则﹣（﹣x+2）=﹣x+2﹣（﹣+x+2），

整理得x2﹣5x+4=0，解得x1=1（舍去），x2=4（舍去），

当0＜x＜4时，PN=MN，则﹣+x+2﹣（﹣x+2）=﹣x+2，

整理得x2﹣5x+4=0，解得x1=1，x2=4（舍去），此时P（1，3）；

当﹣1＜x＜0时，NP=PM，﹣x+2﹣（﹣+x +2）=﹣+x +2

整理得2x2﹣7x﹣4=0，解得x1=﹣，x2=4（舍去），此时P（﹣， ）；

当x＜﹣1时，NM=PM，﹣x+2=﹣（﹣+x +2），

整理得x2﹣2x﹣8=0，解得x1=﹣2，x2=4（舍去），此时P（﹣2，﹣3）；

综上所述，满足条件的P点坐标为（﹣，）或（﹣2，﹣3）或（1，3）．