Question

【题目】某公司有甲种原料，乙种原料，计划用这两种原料生产、两种产品共40件．生产每件种产品需甲种原料，乙种原料，可获利润900元；生产每件种产品需甲种原料，乙种原料，可获利润1100元．设安排生产种产品件(为非负整数)． ．

(I)根据题意，填写下表：

	甲（）	乙（）	件数（件）

(Ⅱ) 安排生产、两种产品的件数有几种方案？试说明理由：

(Ⅲ) 设生产这批40件产品共可获利润元，将表示为的函数，并求出最大利润．

Answer 1

【答案】(I)，；(Ⅱ)共有三种方案，理由见解析；(Ⅲ) 39400．

【解析】

(I)根据总件数=单件需要的原料×件数列式即可；

(Ⅱ)根据两种产品所需要的甲、乙两种原料列出不等式组，然后求解即可；

(Ⅲ)根据总利润等于两种产品的利润之和列式整理，然后根据一次函数的增减性求出最大利润即可．

(I)∵安排生产种产品件，而生产每件种产品需甲种原料，乙种原料，

∴生产种产品件，需要甲种原料为：8x，

∵生产、两种产品共40件，

∴生产B种产品（40-x）件，

∵生产每件种产品需乙种原料，

∴生产B种产品，需要乙种原料为：，

故表格分别填入：A甲种原料8x，B乙种原料9（40-x）；

(Ⅱ)根据题意得，

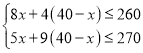
由①得，，

由②得，，

∴不等式组的解集是

∵是正整数，

∴，

共有三种方案:

方案一:产品23件，产品17件，

方案二:产品24件，产品16件；

方案三:产品25件，产品15件；

(Ⅲ) ，

∵，

∴随的增大而减小，

∴时，有最大值．

y最大=-200×23+44000=39400元．