题目内容
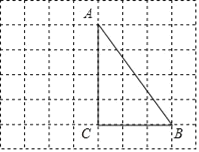
【题目】如图所示，在每个边长都为1的小正方形组成的网格中，点
、
、
均为格点．
（1）线段
的长度等于______；
（2）若
为线段上的动点，以
、
为邻边的四边形
为平行四边形，当
长度最小时，请你借助网格和无刻度的直尺画出该平行四边形，并简要说明你的作图方法：__________（不要求证明）．
【答案】5 取格点
、
、
，连结
与
垂直交于点
，延长
与AB的平行线
交于点Q，四边形
即为所求
【解析】
（1）根据勾股定理即可求得AB的长；
（2）取AC的中点D，过点D作DE⊥AB于点P，过点C作直线CF∥AB，交PD的延长线于点Q，连接AQ、CP，即可画出平行四边形PAQC．
（1）根据网格可知：
线段的长度为
，
所以线段AB的长度等于5．
故答案为5；
（2）如图所示：四边形PAQC即为所求．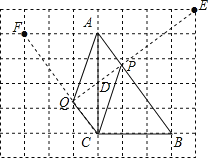
①取AC的中点D，取格点E，使DE⊥AB于点P，
②取格点F，使CF∥AB，交PD的延长线于点Q，
③连接AQ、CP．
练习册系列答案
相关题目
【题目】某农经公司以40元/千克的价格收购一批农产品进行销售，经过市场调查，发现该产品日销售量p（千克）与销售价格x（元/千克）之间满足一次函数关系，部分数据如表：
销售价格x（元/千克） | 40 | 50 | 60 | 70 | 80 |
日销售量p （千克） | 120 | 100 | 80 | 60 | 40 |
（1）求p与x之间的函数表达式；
（2）农经公司应该如何确定这批农产品的销售价格，才能使日销售利润最大?
（3）若农经公司每销售1千克这种农产品需支出m元（m>0）的相关费用，当
时，农经公司的日获利的最大值为1682元，求m的值．（日获利日销售利润日支出费用）