题目内容
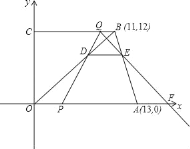
【题目】如图，在直角梯形OABC中，OA∥BC，A、B两点的坐标分别为A（13，0），B（11，12）．动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿x轴向终点A运动，点Q以每秒1个单位的速度沿BC方向运动；当点P停止运动时，点Q也同时停止运动．线段PQ和OB相交于点D，过点D作DE∥x轴，交AB于点E，射线QE交x轴于点F．设动点P、Q运动时间为t（单位：秒）．
(1)当t为何值时，四边形PABQ是平行四边形.
(2)△PQF的面积是否发生变化？若变化，请求出△PQF的面积s关于时间t的函数关系式；若不变，请求出△PQF的面积.
(3)随着P、Q两点的运动，△PQF的形状也随之发生了变化，试问何时会出现等腰△PQF？
【答案】(1)t=
;(2)见解析;(3)见解析.
【解析】
(1)设OP=2t，QB=t，PA=13﹣2t，根据平行四边形的性质（对边平行且相等）知，只需QB=PA，从而求得t；
(2)根据平行线分线段成比例求得
=
；然后由平行线OB∥DE∥PA分线段成比例求得
；利用等量代换求得AF=2QB=2t，PF=OA=13；最后由三角形的面积公式求得△PQF的面积；
(3)由(2)知，PF=OA=13．分三种情况解答：①QP=FQ，作QG⊥x轴于G，则11﹣t﹣2t=2t+13﹣（11﹣t）；②PQ=FP；③FQ=FP．
解：(1)设OP=2t，QB=t，PA=13﹣2t，要使四边形PABQ为平行四边形，则13﹣2t=t
∴
．
(2)不变．
∵，
∴
，
∵QB∥DE∥PA，
∴
，
∴AF=2QB=2t，
∴PF=OA=13，
∴S△PQF=
；
(3)由(2)知，PF=OA=13，
①QP=FQ，作QG⊥x轴于G，则11﹣t﹣2t=2t+13﹣（11﹣t），
∴t=
；
②PQ=FP，
∴
，
∴t=2或
；
③FQ=FP，
∴
，
∴t=1；
综上，当t=或1或2或时，△PQF是等腰三角形．
