题目内容
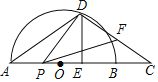
【题目】如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=![]() cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.

【答案】(1)详见解析;(2)![]()
【解析】
(1)首先证明OD∥AC,推出∠ODB=∠C,由OB=OD,推出∠B=∠ODB,即可证明∠B=∠C;
(2)设AC与⊙O相切于点F,连接OF,作AH⊥BC于H,设半径为r.解直角三角形求出AH,由tanC=![]() =2,推出EC=
=2,推出EC=![]() ,推出AF=
,推出AF=![]() -r-
-r-![]() =
=![]() -
-![]() r,在Rt△AOF中,根据OA2=AF2+OF2,构建方程即可解决问题.
r,在Rt△AOF中,根据OA2=AF2+OF2,构建方程即可解决问题.
(1)连接OD,
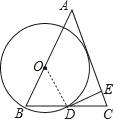
∵DE是⊙O的切线,
∵DE⊥OD,
∵AC⊥DE,
∴OD∥AC,
∴∠ODB=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠B=∠C,
∴AB=AC;
(2)设AC与⊙O相切于点F,连接OF,作AH⊥BC于H,设半径为r,
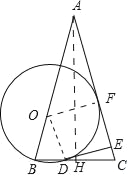
∵AB=AC,AH⊥BC,
∴BH=CH=1,
∴AH=![]() =2,
=2,
∴tan∠C=![]() =2,
=2,
∵∠OFE=∠ODE=∠DEF=90°,
∴四边形ODEF是矩形,
∵OD=OF,
∴四边形ODEF是正方形,
∴EF=DE=r,
∵tanC=![]() =2,
=2,
∴EC=![]() ,
,
∴AF=![]() ﹣r﹣
﹣r﹣![]() r=
r=![]() ﹣
﹣![]() r,
r,
在Rt△AOF中,∵OA2=AF2+OF2,
∴(![]() ﹣r)2=r2+(
﹣r)2=r2+(![]() ﹣
﹣![]() r)2,
r)2,
解得r=![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目