Question

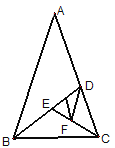
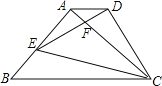
【题目】如图，△ABC为等腰直角三角形，∠BAC=90°，BC=1，E为AB上任意一动点，以CE为斜边作等腰Rt△CDE，连结AD，下列说法：①∠BCE=∠ACD；②△ACD∽△BCE；③△AED∽△ECB；④AD∥BC；⑤四边形ABCD的面积有最大值，且最大值为.其中正确的结论是_________.

Answer 1

【答案】①②④⑤

【解析】

①首先根据等腰三角形的性质得到∠ACB=∠DCE=45°，从而得到∠ACB﹣∠ACE=∠DCE﹣∠ACE，进而得到结论：∠ECB=∠DCA正确；②利用两组对应边成比例，夹角相等的三角形相似证得结论△ADC∽△BEC即可；④证得△ADC∽△BEC后得到∠DAC=∠B=45°，从而得到∠DAC=∠BCA=45°，即AD∥BC；③由④知：△EAD与△BEC不相似，故③错误；⑤△ABC的面积为定值，若梯形ABCD的面积最大，则△ACD的面积最大；△ACD中，AD边上的高为定值（即为1），若△ACD的面积最大，则AD的长最大；由④的△BEC∽△ADC知：当AD最长时，BE也最长；故梯形ABCD面积最大时，E、A重合，此时EC=AC=，AD=，故S梯形ABCD=（1+）×=，从而判定是否正确即可；

∵△ABC、△DCE都是等腰直角三角形，

∴AB=AC=BC=，CD=DE=CE；∠B=∠ACB=∠DEC=∠DCE=45°；

①∵∠ACB=∠DCE=45°，

∴∠ACB﹣∠ACE=∠DCE﹣∠ACE；

即∠ECB=∠DCA；故①正确；

②==，

∴=；

由①知∠ECB=∠DCA，

∴△BEC∽△ADC；故②正确；

④由②得△BEC∽△ADC，

∴∠DAC=∠B=45°；

∴∠DAC=∠BCA=45°，即AD∥BC，故④正确；

③由④知：∠DAC=45°，则∠EAD=135°；

∠BEC=∠EAC+∠ECA=90°+∠ECA；

∵∠ECA＜45°，

∴∠BEC＜135°，即∠BEC＜∠EAD；

因此△EAD与△BEC不相似，故③错误；

⑤△ABC的面积为定值，若梯形ABCD的面积最大，则△ACD的面积最大；

△ACD中，AD边上的高为定值（即为1），若△ACD的面积最大，则AD的长最大；

由④的△BEC∽△ADC知：当AD最长时，BE也最长；

故梯形ABCD面积最大时，E、A重合，此时EC=AC=，AD=；

故S梯形ABCD=（1+）×=，故⑤正确；

故正确的结论是①②④⑤，

故答案为：①②④⑤