Question

【题目】如图，抛物线与x轴交于点A，B，与轴交于点C。过点C作CD∥x轴，交抛物线的对称轴于点D，连结BD。已知点A坐标为（-1，0）。

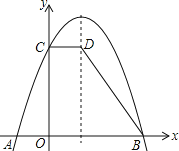
（1）求该抛物线的解析式；

（2）求梯形COBD的面积。

Answer 1

【答案】（1）（2）

【解析】解：（1）将A（―1，0）代入中，得：0=4a+4，解得：a=－1。

∴该抛物线解析式为。

（2）对于抛物线解析式，令x=0，得到y=3，即OC=3，

∵抛物线的对称轴为直线x=1，∴CD=1。

∵A（－1，0），∴B（3，0），即OB=3。

∴。

（1）将A坐标代入抛物线解析式，求出a的值，即可确定出解析式。

（2）抛物线解析式令x=0求出y的值，求出OC的长，根据对称轴求出CD的长，令y=0求出x的值，确定出OB的长，根据梯形面积公式即可求出梯形COBD的面积。