题目内容
已知直线y=2x+4与x轴、y轴的交点分别为A、B,y轴上点C的坐标为(0,2),在x轴的正半轴上找一点P,使以P、O、C为顶点的三角形与△AOB相似,则点P的坐标为______.
如图,
∵直线y=2x+4,
∴当x=0时,y=4;
当y=0时,x=-2.
∴A(-2,0),B(0,4),
∴OA=2,OB=4,
∵C的坐标为(0,2),
∴OC=2,
若以P、O、C为顶点的三角形与△AOB相似,
那么有两种情况:
①OC和OA对应,那么OP和OB对应,
∵OA=OC=2,
∴OP=OB=4,
∴P的坐标为(4,0);
②OC和OB对应,那么OP和OA对应,
∴
=
,
∴OP=1,
∴P的坐标为(1,0).
因此P的坐标为(4,0)或(1,0).
故填空答案:(4,0)或(1,0).
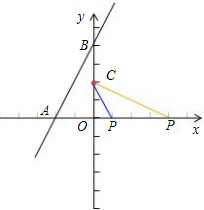
∵直线y=2x+4,
∴当x=0时,y=4;
当y=0时,x=-2.
∴A(-2,0),B(0,4),
∴OA=2,OB=4,
∵C的坐标为(0,2),
∴OC=2,
若以P、O、C为顶点的三角形与△AOB相似,
那么有两种情况:
①OC和OA对应,那么OP和OB对应,
∵OA=OC=2,
∴OP=OB=4,
∴P的坐标为(4,0);
②OC和OB对应,那么OP和OA对应,
∴
| OC |
| OB |
| OP |
| OA |
∴OP=1,
∴P的坐标为(1,0).
因此P的坐标为(4,0)或(1,0).
故填空答案:(4,0)或(1,0).
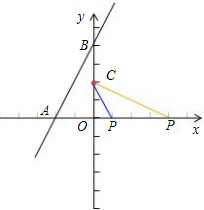

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



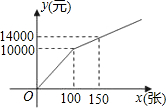

 当两车油箱中剩余油量相同时,那么两车的行驶路程相差多少千米?
当两车油箱中剩余油量相同时,那么两车的行驶路程相差多少千米?