��Ŀ����
��ͼ����ƽ��ֱ������ϵxOy�У�Rt��ABC��A��B����������x���ϣ�����C��y��ĸ������ϣ���֪OA=4OB��AC=2BC=2
��
��1�����A��B��C�����ꣻ
��2������C����ԭ��ĶԳƵ�ΪC�䣬������AB�Ĵ�ֱƽ�������Ƿ����һ��G��ʹ�á�GBC����ܳ���С�������ڣ������G���������С�ܳ����������ڣ���˵�����ɣ�
��3�����P��ֱ��BC�����ڵ�B����C��һ�����㣬����P��x���ƽ���߽�ֱ��AC�ڵ�Q������Q��QM��ֱ��x���ڵ�M���ٹ���P��PN��ֱ��x���ڵ�N���õ�����PQMN�����ڵ�P���˶������У�������PQMNΪ������ʱ����������εı߳���

| 5 |
��1�����A��B��C�����ꣻ
��2������C����ԭ��ĶԳƵ�ΪC�䣬������AB�Ĵ�ֱƽ�������Ƿ����һ��G��ʹ�á�GBC����ܳ���С�������ڣ������G���������С�ܳ����������ڣ���˵�����ɣ�
��3�����P��ֱ��BC�����ڵ�B����C��һ�����㣬����P��x���ƽ���߽�ֱ��AC�ڵ�Q������Q��QM��ֱ��x���ڵ�M���ٹ���P��PN��ֱ��x���ڵ�N���õ�����PQMN�����ڵ�P���˶������У�������PQMNΪ������ʱ����������εı߳���

��1����OB=k��k��0������OA=4k��AB=5k��
��AC=2BC=2
����ACB=90�㣬
�ࣨ2
��2+��
��2=��5k��2��
��ã�k=1��
��OB=1��OA=4��
��A��-4��0����B��1��0����
��OC=
=2��
��C��0��-2����
��2����ͼ1������AC�䣬�ɼ���֪ʶ֪AC����AB�Ĵ�ֱƽ����l�Ľ��㼴Ϊ��GBC����ܳ���Сʱ�ĵ�G��
����GB��BC�䣬
�ߵ�C�����C����ԭ��Գƣ���C��0��-2����
��C�䣨0��2����
��A��-4��0����B��1��0����
��ֱ��AC��Ľ���ʽΪ��y=
x+2��
ֱ��l�Ľ���ʽΪ��x=-
��
���G��-
��
����
��BC��=
=
��AC��=
=2
���GBC�����С�ܳ�Ϊ��
GB+GC��+BC��=AC��+BC��=3
��
��3����ͼ��֪��P��������ֱ��BC�ĵ�B���Ϸ���
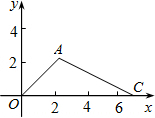
����P���߶�BC֮��ʱ����ͼ2����
��������PQMN�ı߳�Ϊt��
��A��-4��0����B��1��0����C��0��-2��
��ֱ��AC�Ľ���ʽΪ��y=-
x-2��
ֱ��BC�Ľ���ʽΪ��y=2x-2��
���P��
��-t������Q��2t-4��-t����
���N��
��0������M��2t-4��0����
��MN=-2t+4+
=t�����t=
��
����P��ֱ��BC�����·�ʱ��ͬ���ɵõ�N��
��0������M��2t-4��0������ʱ
MN=2t-4-
=t�����t=
��
����������������PQMN�ı߳�Ϊ
��
��

��AC=2BC=2
| 5 |
�ࣨ2
| 5 |
| 5 |
��ã�k=1��
��OB=1��OA=4��
��A��-4��0����B��1��0����
��OC=
| CB2+OB2 |
��C��0��-2����
��2����ͼ1������AC�䣬�ɼ���֪ʶ֪AC����AB�Ĵ�ֱƽ����l�Ľ��㼴Ϊ��GBC����ܳ���Сʱ�ĵ�G��
����GB��BC�䣬
�ߵ�C�����C����ԭ��Գƣ���C��0��-2����
��C�䣨0��2����
��A��-4��0����B��1��0����
��ֱ��AC��Ľ���ʽΪ��y=
| 1 |
| 2 |
ֱ��l�Ľ���ʽΪ��x=-
| 3 |
| 2 |
���G��-
| 3 |
| 2 |
| 5 |
| 4 |
��BC��=
| 12+22 |
| 5 |
| 42+22 |
| 5 |
���GBC�����С�ܳ�Ϊ��
GB+GC��+BC��=AC��+BC��=3
| 5 |
��3����ͼ��֪��P��������ֱ��BC�ĵ�B���Ϸ���
����P���߶�BC֮��ʱ����ͼ2����

��������PQMN�ı߳�Ϊt��
��A��-4��0����B��1��0����C��0��-2��
��ֱ��AC�Ľ���ʽΪ��y=-
| 1 |
| 2 |
ֱ��BC�Ľ���ʽΪ��y=2x-2��
���P��
| 2-t |
| 2 |
���N��
| 2-t |
| 2 |
��MN=-2t+4+
| 2-t |
| 2 |
| 10 |
| 7 |
����P��ֱ��BC�����·�ʱ��ͬ���ɵõ�N��
| 2-t |
| 2 |
MN=2t-4-
| 2-t |
| 2 |
| 10 |
| 3 |
����������������PQMN�ı߳�Ϊ
| 10 |
| 7 |
| 10 |
| 3 |


��ϰ��ϵ�д�
 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�����Ŀ
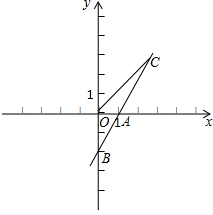

 ��A��B���㣮
��A��B���㣮

 ����ѪҺ�к�ҩ��y��ʱ��t֮�����������ͼ��ʾ���ߣ�
����ѪҺ�к�ҩ��y��ʱ��t֮�����������ͼ��ʾ���ߣ�