题目内容
【题目】如图,经过抛物线y=x2+x﹣2与坐标轴交点的圆与抛物线另交于点D,与y轴另交于点E,则∠BED=_____.
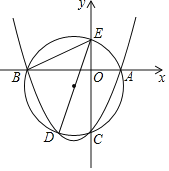
【答案】45°
【解析】
连接AD,作DM⊥AB于M,根据抛物线的解析式求得与坐标轴的交点坐标,进而求得D的坐标,即可得到AM=DM=2,从而求得∠BAD=45°,根据圆周角定理即可求得∠BED的度数.
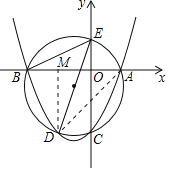
解:连接AD,作DM⊥AB于M,
在抛物线y=x2+x﹣2中,令y=0,则x2+x﹣2=0,解得x=﹣2或x=1,
∴A(1,0),B(﹣2,0),
令x=0,则y=﹣2,
∴C(0,﹣2),
∴抛物线的对称轴为直线x=![]() ,
,
∴D(﹣1,﹣2),
∴M(﹣1,0),
∵DM=2,AM=2,
∴∠BAD=∠ADM=45°,
∵∠BED=∠BAD,
∴∠BED=45°.
故答案为45°.

练习册系列答案
相关题目