题目内容
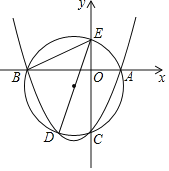
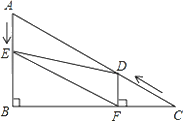
【题目】如图,平面直角坐标系中两条直线OC⊥BC,垂足为C,其OC=2cm,∠COB=60°,反比例函数y=![]() 的图象过点C.
的图象过点C.
(1)求:反比例函数表达式和点B的坐标.
(2)若现有长为1cm的线段MN在线段OB上沿OB方向以1cm/s的速度向点B运动(运动前点M与点O重合,N到点B停止运动),过M、N作OB的垂线分别交直线OC、BC于P、Q两点,线段MN运动的时间为ts.
①若△OMP的面积为S.求出当0<t≤1时,S与t的函数关系式.
②线段MN运动过程中,四边形MNQP有可能成为矩形吗?若可能,直接写出此时t的值;若不可能,说明理由.
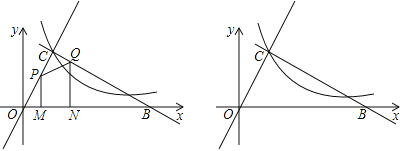
【答案】(1)y=![]() ,B(4,0);(2)①S=
,B(4,0);(2)①S=![]() t2;②可能,t=
t2;②可能,t=![]() .
.
【解析】
(1)过点C作CD⊥OB于点D,在Rt△ODC中运用三角函数可求出点C的坐标,然后将点C的坐标代入y=![]() ,就可得到反比例函数表达式,然后在Rt△OCB中运用三角函数就可求出点B的坐标;
,就可得到反比例函数表达式,然后在Rt△OCB中运用三角函数就可求出点B的坐标;
(2)由题可得:OM=t,MN=1,ON=t+1.①只需用t的代数式表示出PM,就可解决问题;②分别表示出PM、QN的长(用t的代数式),根据四边形MNQP为矩形时PM=QN建立关于t的方程,解这个方程就可得到t的值.
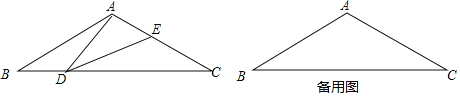
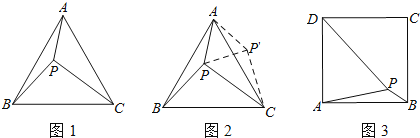
解:(1)过点C作CD⊥OB于点D,如图1.
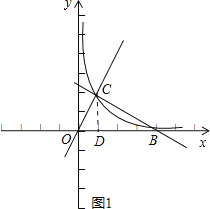
在Rt△ODC中,
∵OC=2,∠COD=60°,
∴CD=OCsin∠COD=2×![]() =
=![]() ,
,
OD=OCcos∠COD=2×![]() =1,
=1,
∴点C的坐标为(1,![]() ).
).
∵反比例函数y=![]() 的图象过点C,
的图象过点C,
∴k=1×![]() =
=![]() ,
,
∴反比例函数的解析式为y=![]() .
.
∵OC⊥BC,
∴cos∠COB=![]() ,即
,即![]() =
=![]() ,
,
∴OB=4,
∴点B的坐标为(4,0);
(2)由题可得:OM=1×t=t,MN=1,ON=t+1.
①当0<t≤1时,
∵点C(1,2),
∴点P在线段OC上,如图2.
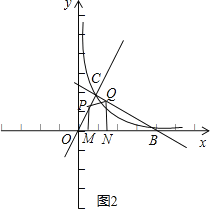
在Rt△OMP中,
PM=OMtan∠POM=![]() t,
t,
∴S=![]() OMPM=
OMPM=![]() ×t×
×t×![]() t=
t=![]() t2;
t2;
②t的值为![]() .
.
解题思路:求出直线OC的解析式,为y=![]() x;
x;
求出直线BC的解析式,为y=﹣![]() x+
x+![]() ;
;
从而得到PM=![]() t,QN=﹣
t,QN=﹣![]() (t+1)+
(t+1)+ ![]() ;
;
若四边形MNQP是矩形,则有PM=QN,如图3,
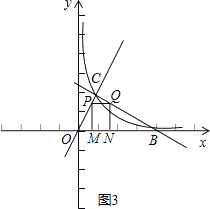
则![]() t=﹣
t=﹣![]() (t+1)+
(t+1)+ ![]() ,
,
解得:t=![]() ,
,
此时点M、点N都在线段OB上,符合条件.

【题目】小东根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是__________________
的自变量x的取值范围是__________________
(2)如表示y与x的几组对应值:
x | … |
|
|
|
|
|
|
|
|
|
|
| … |
y | … |
|
|
|
|
|
|
|
|
|
| m | … |
表中m的值为____________
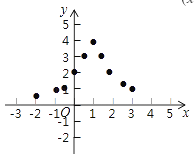
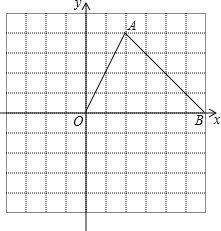
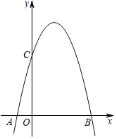
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数![]() 的大致图像;
的大致图像;
(4)结合函数图像,请写出函数![]() 的2条性质:
的2条性质:
①__________________________________________________________________________
②__________________________________________________________________________
(5)解决问题:如果函数![]() 与直线
与直线![]() 的交点有2个,那么a的取值范围是_______________________
的交点有2个,那么a的取值范围是_______________________
(6)![]() 在函数图像上,若
在函数图像上,若![]() ,则m的取值范围______________
,则m的取值范围______________