题目内容
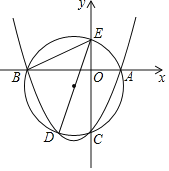
【题目】已知:如图,直线y=x﹣15与x轴、y轴分别相交于点A和点B.抛物线![]() 经过A、B两点.
经过A、B两点.
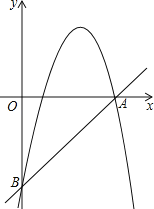
(1)求这个抛物线的解析式;
(2)若这抛物线的顶点为点D,与x轴的另一个交点为点C.对称轴与x轴交于点H,求△DAC的面积;
(3)若点E是线段AD的中点.CE与DH交于点G,点P在y轴的正半轴上,△POH是否能够与△CGH相似?如果能,请求出点P的坐标;如果不能,请说明理由.
【答案】(1)y=﹣![]() x2+6x﹣15;(2)△DAC的面积为72;(3)△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或P2(0,
x2+6x﹣15;(2)△DAC的面积为72;(3)△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或P2(0,![]() ).
).
【解析】
(1)利用一次函数的解析式,求得A、B的坐标,再代入抛物线得出方程组,即可求出抛物线的解析式;
(2)分别求出点D、点C的坐标,根据三角形的面积公式即可求得答案;
(3)根据题目的条知点G是△DAC的重心,首先求得![]() 的值,再根据相似三角形的性质得出两个比例式,代入即可求得点P的坐标.
的值,再根据相似三角形的性质得出两个比例式,代入即可求得点P的坐标.
(1)∵y=x﹣15,
y=0时,0=x﹣15,
∴x=15,
当x=0时,y=﹣15,
∴A(15,0),B(0,﹣15),
代入得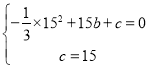 ,
,
解得![]() ,
,
∴抛物线的解析式:![]() .
.
(2)抛物线的解析式可变形为![]() ,
,
∴顶点D坐标为(9,12),
设y=0,则![]() ,
,
∴(x﹣9)2=36.
∴x1=3,x2=15,
∴点C的坐标为(3,0),
∴![]() .
.
(3)∵点E是线段AD的中点,点H是线段AC的中点,.
∴点G是△DAC的重心.如图:
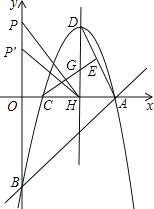
∵顶点D坐标为(9,12),
∴![]() ,
,
∴HO=9,CH=6.
设△POH∽△GHC时,
![]() ,
,
∴![]()
∴PO=6,
∴P1(0,6);
△POH∽△CHG时,![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .
.
∴△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或![]() .
.

 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】小东根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是__________________
的自变量x的取值范围是__________________
(2)如表示y与x的几组对应值:
x | … |
|
|
|
|
|
|
|
|
|
|
| … |
y | … |
|
|
|
|
|
|
|
|
|
| m | … |
表中m的值为____________
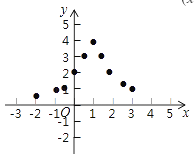
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数![]() 的大致图像;
的大致图像;
(4)结合函数图像,请写出函数![]() 的2条性质:
的2条性质:
①__________________________________________________________________________
②__________________________________________________________________________
(5)解决问题:如果函数![]() 与直线
与直线![]() 的交点有2个,那么a的取值范围是_______________________
的交点有2个,那么a的取值范围是_______________________
(6)![]() 在函数图像上,若
在函数图像上,若![]() ,则m的取值范围______________
,则m的取值范围______________