Question

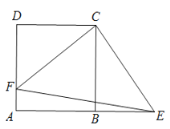
【题目】如图，正方形ABCD的面积是64，点F在边AD上，点E在边AB的延长线上．若CE⊥CF，且△CEF的面积是50，则DF的长度是____ ．

Answer 1

【答案】6

【解析】

根据等角的余角相等判断出∠ECB=∠FCD,又知∠CDF=∠CBE=90°,DC=CB,可得△DCF≌△BCE,从而得出CF=CE,根据三角形的面积公式求出三角形的边长,再利用勾股定理求出DF的长.

∵四边形ABCD是正方形,
∴CD=CB==8,∠D=∠CBE=90°,
∵CE⊥CF,
∴∠DCF+∠FCB=90°,∠ECB+∠FCB=90°,
∴∠DCF=∠ECB,
∴△DCF≌△BCE.
∴CF=CE,
由△CEF的面积是50,可得CF=CE==10,
在Rt△CDF中,DF===6.
故答案为：6.