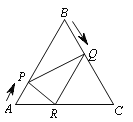
题目内容
【题目】如图，在△ABC和△DEF中，AB∥DE，点A，F，C，D在同一直线上，AF＝CD，∠AFE＝∠BCD．
试说明：
（1）△ABC≌△DEF；
（2）BF∥EC．
【答案】（1）见解析；（2）见解析.
【解析】
（1）由平行线的性质，根据全等三角形的判定（ASA）即可得到答案；
（2）根据全等三角形的性质和判定（SAS）进行证明即可得到答案.
（1）∵AB∥DE，∴∠A＝∠D
∵AF＝CD，∴AF+FC＝CD+FC 即 AC＝DF
∵∠AFE＝∠BCD，∴∠DFE＝∠ACB
在△ABC和△DEF中，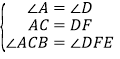
∴△ABC≌△DEF （ASA）
（2）∵△ABC≌△DEF
∴BC＝EF
在△BCF和△EFC中，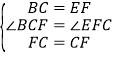
∴△BCF≌△EFC （SAS）
∴∠BFC＝∠ECF
∴BF∥EC
练习册系列答案
相关题目
【题目】抛物线
上部分点的横坐标
， 纵坐标
的对应值如下表：
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法正确的是 ．
①抛物线与轴的一个交点为
； ②抛物线与轴的交点为
；
③抛物线的对称轴是：直线
； ④在对称轴左侧随增大而增大.
