题目内容
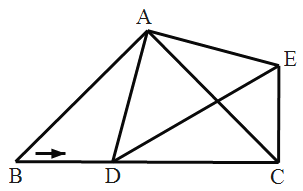
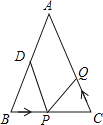
【题目】如图所示,已知△ABC中,AB=AC=10,BC=8,点D是AB中点,点P在线段BC上以每秒3个单位长度的速度由点B向点C运动,同时点Q在线段CA上由点C向点A以每秒a个单位长度的速度运动.设运动的时间为t秒.
(1)求CP的长(用含t的式子表示);
(2)若以点C、P、Q为顶点的三角形和以点B、D、P为顶点的三角形全等,并且∠B和∠C是对应角,求a和t的值.
【答案】(1)8-3t;(2)t=![]() ,a=
,a=![]() 或t=1,a=3
或t=1,a=3
【解析】
(1)用BC的长度减去BP的长度即可;
(2)根据全等三角形对应边相等,列方程即可得到结论.
(1)∵BC=8,
∴CP=8﹣3t
(2)分两种情况:
①当△CPQ≌△BPD时,BP=CP,8﹣3t=4,
t=![]() ;
;
BD=CQ,![]() a=5,
a=5,
∴a=![]()
②当△CPQ≌△BDP时,CP=BD,8﹣3t=5,
t=1;
CQ=BP,
∴a=3.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目