题目内容
【题目】如图，在矩形ABCD中，AD=10，E为AB上一点，且AE= 
AB=a，连结DE，F是DE中点，连结BF，以BF为直径作⊙O．
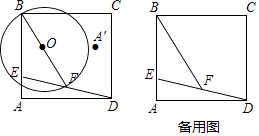
（1）用a的代数式表示DE2= ， BF2=；
（2）求证：⊙O必过BC的中点；
（3）若⊙O与矩形ABCD各边所在的直线相切时，求a的值；
（4）作A关于直线BF的对称点A′，若A′落在矩形ABCD内部（不包括边界），则a的取值范围 ． （直接写出答案）
【答案】
（1）a2+100,
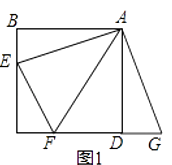
（2）证明：如图1，设⊙O交BC于H，连接FH，
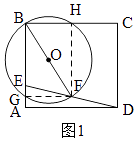
∵BF是⊙O的直径，
∴∠BHF=90°，
∴∠ABC=∠BHF=∠AGF=90°，
∴四边形BGFH是矩形，
∴BH=GF= 
AD= BC，
∴H是BC的中点，
即：⊙O必过BC的中点
（3）解：分两种情况：
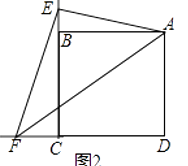
①如图2，当⊙O与边CD相切时，设切点为M，连接OM、FH交于N，则OM⊥CD，
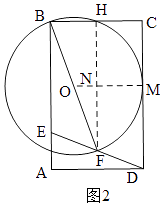
∴OM=ON+MN= 
+5= 
，
∵OM⊥FH，
∴NF= FH= × 
= 
a，
Rt△ONF中，ON2+NF2=OF2=OM2，
∴ 
+（ 
）2= 
，
a= 
，
∵a＞0，
∴a= 
，
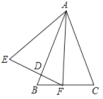
②如图3，当⊙O与边AD相切时，设切点为Q，
连接OQ，则OQ⊥AD，连接FG，交OQ于P，
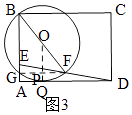
∴OQ=OP+PQ= BG+AG= + 
= 
a，
由（1）知： 
且BF=2OQ，
∴25+ 
a2=（2× a）2，
a= 
，
综上所述，若⊙O与矩形ABCD各边所在的直线相切时，a的值为 或
（4）
＜a＜ 
【解析】解：（1）如图1，∵四边形ABCD是矩形，
∴∠A=90°，
在Rt△AED中，AE=a，AD=10，
由勾股定理得：ED2=AE2+AD2=a2+102=a2+100，
设⊙O交AB于G，连接FG，
∵BF是⊙O的直径，
∴∠BGF=90°，
∵∠A=90°，
∴∠BGF=∠A，
∴FG∥AD，
∵F是ED的中点，
∴GF= AD=5，EG=AG= a，
∵AE= 
AB=a，
∴AB=4a，
∴BG=4a﹣ a= a，
由勾股定理得：BF2=BG2+GF2，
∴BF2= 
+52= 
+25= ，
所以答案是：a2+100； ；
⑷如图4，当A的对称点A′恰好在边BD上时，连接AA′交BF于H，连接AF、A′F，过F作MN⊥BC，交BC于M，交AD于N，则MN⊥AD，
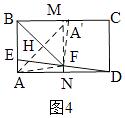
∵A关于直线BF的对称点A′，
∴BF是AA′的垂直平分线，
∴AF=A′F，AB=A′B=4a，
由（1）（2）得：FN= a，FM= a，A′M=4a﹣5，AN=5，
由勾股定理得： 
=（4a﹣5）2+ ，
解得：a1=0（舍），a2= ，
∴当a＜ 时，A′落在矩形ABCD外部（包括边界），
如图5，当A′落在边CD上时，连接AA′、A′B，过F作MG⊥AB，则MG⊥CD，
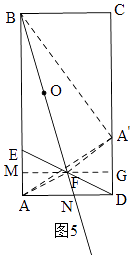
设射线BF交AD于N，
易得A′G=AM=DG= a，A′C=3a，
∵BF是AA′的垂直平分线，
∴AB=A′B，
则（4a）2=102+（3a）2，
a= ，
∴a的取值范围是： ＜a＜ ，
所以答案是： ＜a＜ ．
【考点精析】根据题目的已知条件，利用线段垂直平分线的性质和勾股定理的概念的相关知识可以得到问题的答案，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
