题目内容
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.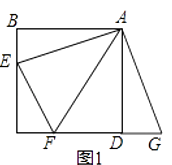
(1)【类比引申】如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;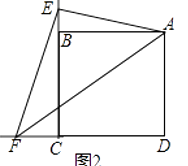
(2)【联想拓展】如图4,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
【答案】
(1)解: DF=EF+BE.
理由:如图(1)所示,
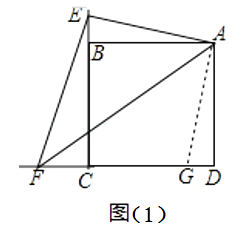
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∵∠ADC=∠ABE=90°,
∴点C、D、G在一条直线上,
∴EB=DG,AE=AG,∠EAB=∠GAD,
∵∠BAG+∠GAD=90°,
∴∠EAG=∠BAD=90°,
∵∠EAF=45°,
∴∠FAG=∠EAG﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠GAF,
在△EAF和△GAF中,
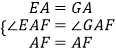 ,
,
∴△EAF≌△GAF,
∴EF=FG,
∵FD=FG+DG,
∴DF=EF+BE;
(2)解:∵∠BAC=90°,AB=AC,
∴将△ABE绕点A顺时针旋转90°得△ACG,连接FG,如图(2),
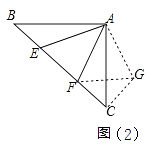
∴AG=AE,CG=BE,∠ACG=∠B,∠EAG=90°,
∴∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°,
∴FG2=FC2+CG2=BE2+FC2;
又∵∠EAF=45°,
而∠EAG=90°,
∴∠GAF=90°﹣45°,
在△AGF与△AEF中,
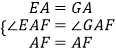 ,
,
∴△AEF≌△AGF,
∴EF=FG,
∴CF2=EF2﹣BE2=52﹣32=16,
∴CF=4.
【解析】(1)类比题干的思路方法,仍是把△ABE绕点A逆时针旋转90°至△ADG,由旋转的性质可得△EAF≌△GAF,由FD=FG+DG,可得DF=EF+BE;(2)类比(1),仍是旋转法:将△ABE绕点A顺时针旋转90°得△ACG,仍可证△AEF≌△AGF,可得EF=FGCF2=EF2﹣BE2=52﹣32=16,得CF=4.
【考点精析】根据题目的已知条件,利用旋转的性质的相关知识可以得到问题的答案,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

 小学课时特训系列答案
小学课时特训系列答案【题目】凤凰景区的团体门票的价格规定如下表
购票人数 | 1~55 | 56~110 | 111~165 | 165以上 |
价格(元/人) | 10 | 9 | 8 | 7 |
某校七年级(1)班和(2)班共112人去凤凰景区进行研学春游活动,当两班都以班为单位分别购票,则一共需付门票1060元.
(1)你认为由更省钱的购票方式吗?如果有,能节省多少元?
(2)若(1)班人数多于(2)班人数,求(1)(2)班的人数各是多少?
(3)若七年级(3)班53人也一同前去春游时,如何购票显得更为合理?请你设计一种更省钱的方案,并求出七年级3个班共需付门票多少元?