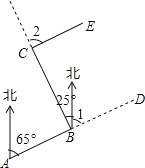
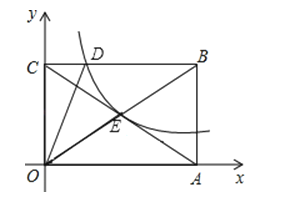
��Ŀ����
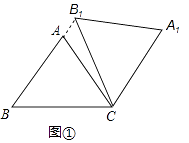
����Ŀ����ͼ���ڳ���Ϊ1����λ���ȵ�С��������ɵ������������У���ABC����������A��B��C���ڸ���ϣ�
��1����ͼ�л������ABC����ֱ��l����ԳƵġ�A1B1C1��
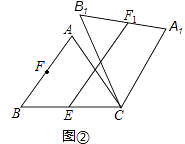
��2����ֱ��l���ҳ�һ��P��ʹ��|PA��PC|��ֵ���������ͼ�ۼ���������ĸP��
��3����ֱ��l���ҳ�һ��Q��ʹ��QA+QC1��ֵ��С����������ͼ�ۼ���������ĸQ��
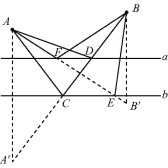
��4���������������д����� ������㣬ʹ�øø����B��C���㹹����BCΪ�ױߵĵ��������Σ�

���𰸡���1������������2������������3������������4��4
��������
��1���ֱ�����A��B��C�Ķ�Ӧ��A1��B1��C1���ɣ�
��2������AC1���ӳ�AC1��ֱ��l�ڵ�P����P��Ϊ����
��3��ֱ��AC��ֱ��l�Ľ���Q��Ϊ����
��4�����߶�BC�Ĵ�ֱƽ���ߣ���ͼD1��D2��D3��D4��Ϊ����
�⣺��1����A1B1C1��ͼ��ʾ��
�ɶԳƵ����ʣ��ֱ�����A��B��C�Ķ�Ӧ��A1��B1��C1��˳������A1B1��A1 C1��B1C1��
�õ���A1B1C1����ABC����ֱ��l����Գƣ�
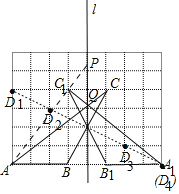
��2����C��C1����ֱ��l�Գƣ�
��PC=PC1��
��|PA��PC|=|PA��PC1|����P��A��C1���㹲��ʱ��|PA��PC1|ȡ�����ֵ����|PA��PC|��ֵ���
������AC1���ӳ�AC1��ֱ��l�ڵ�P����P��Ϊ����
��3����C��C1����ֱ��l�Գƣ�
��QC=QC1��
��QA+QC1=QA+QC����A��Q��C���㹲��ʱ��QA+QCȡ����Сֵ����QA+QC1��ֵ��С��
��ֱ��AC��ֱ��l�Ľ���Q��Ϊ����
��4���߹�����BCΪ�ױߵĵ��������Σ�
����������εĶ������߶�BC�Ĵ�ֱƽ�����ϣ�
�����߶�BC�Ĵ�ֱƽ���ߣ���ͼD1��D2��D3��D4��Ϊ����4����㣻
�ʴ�Ϊ4��

����Ŀ��ijУ�ԡ�ѧ����ѧУ���ֻ�Ӱ��ѧϰ������������˵��飬��������˲���ѧ�����Դ�����Ŀ�����Ϊ���������û��Ӱ�졢Ӱ�첻��Ӱ��ܴ������������Ƴ����²�������ͳ�Ʊ�������ͳ��ͼ������ͳ��ͼ���ṩ����Ϣ������������⣺
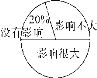
����ͳ�Ʊ����£�
���� | û��Ӱ�� | Ӱ�첻�� | Ӱ��ܴ� |
ѧ������(��) | 20 | 30 | a |
��1��ͳ�Ʊ��е�a������������
��2������ݱ��е����ݣ�̸̸��Ŀ�����������2����