题目内容
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
【答案】
(1)解:∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2.
∴抛物线的表达式为y=x2+2x﹣3
(2)解:y=x2+2x﹣3=(x+1)2﹣4.
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,
∴当x=﹣1,y最小=﹣4.
当x=﹣4时,y=5.
∴﹣4<x<1时,y的取值范围是﹣4≤y<5
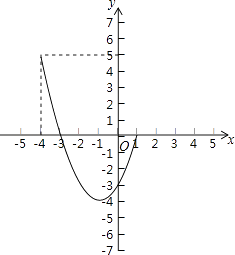
(3)解:y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0).
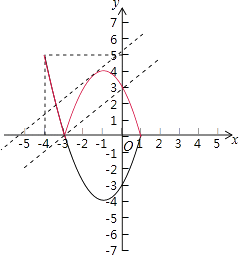
新图象M如右图红色部分.
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b= ![]() .
.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b< ![]() .
.
【解析】(1)把点(1,0)代入抛物线解析式得到关于m的方程,从而可求得m的值,将m的值代入可得到抛物线的表达式;
(2)先求得抛物线的顶点坐标和对称轴,然后画出大致图像,最后,依据函数图像进行判断即可;
(3)根据题意作出函数图象,然后由函数图像可确定新图象M与直线有三个交点时的界点,然后利用待定系数法求解即可.
【考点精析】本题主要考查了二次函数的性质和二次函数图象的平移的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.