Question

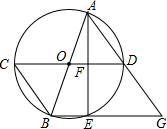
如图，AB、CD是⊙O的直径，弦AE⊥CD于点F，延长BE、AD交于点G．
（1）求证：CD∥BG；
（2）若BE=4，OF=

1

2

DF；
①求证：DF=BE．
②求tanG的值．

Answer 1

（1）证明：∵AB是⊙O的直径，
∴AE⊥BE，
∵AE⊥CD，
∴CD∥BG．

（2）证明：①∵直径CD⊥AE于点F，
∴AF=FE，
又∵AO=BO，
∴OF=

1

2

BE=

1

2

×4=2，
∵OF=

1

2

DF，
∴DF=BE=4．

②∵AO=OD=OF+DF=6，
∴AF=

AO2-OF2

=

62-22

=4

2

，
∵CD∥BG，
∴tanG=tan∠ADF=

AF

FD

=

4 2

4

=

2

．