��Ŀ����
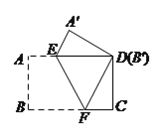
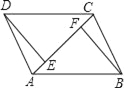
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=8����BAD=60�㣬��E�ӵ�A��������AB��ÿ��2����λ���ȵ��ٶ����յ�B�˶�������E�����A�غ�ʱ������E��EF��AD�ڵ�F����EG��AD��AC�ڵ�G������G��GH��AD��AD����AD���ӳ��ߣ��ڵ�H���õ�����EFHG�����E�˶���ʱ��Ϊt��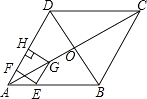
��1�����߶�EF�ij����ú�t�Ĵ���ʽ��ʾ����
��2�����H���D�غ�ʱt��ֵ��
��3�������EFHG������ABCD�ص�����ͼ�ε������Sƽ����λ����S��t֮��ĺ�����ϵʽ��
��4������EFHG�ĶԽ���EH��FG�ཻ�ڵ�O�䣬��OO���ADʱ��t��ֵΪ����OO���ADʱ��t��ֵΪ ��
���𰸡�
��1��
�⣺������֪��AE=2t��0��t��4��
�ߡ�BAD=60�㣬��AFE=90�㣬
��sin��BAD= ![]() ��
��
��EF= ![]() t
t
��2��
�⣺��AE=2t����AEF=30�㣬
��AF=t��
��H��D�غ�ʱ��
��ʱFH=8��t��
��GE=8��t��
��EG��AD��
���EGA=30�㣬
���ı���ABCD�����Σ�
���BAC=30�㣬
���BAC=��EGA=30�㣬
��AE=EG��
��2t=8��t��
��t= ![]()
��3��
�⣺��0��t�� ![]() ʱ��
ʱ��
��ʱ����EFHG������ABCD�ص�����ͼ��Ϊ����EFHG��
���ɣ�2����֪��AE=EG=2t��
��S=EFEG= ![]() t2t=2
t2t=2 ![]() t2��
t2��
�� ![]() ��t��4ʱ����ͼ1��
��t��4ʱ����ͼ1��
��CD��HG���ڵ�I��
��ʱ����EFHG������ABCD�ص�����ͼ��Ϊ�����FEGID��
��AE=2t��
��AF=t��EF= ![]() t��
t��
��DF=8��t��
��AE=EG=FH=2t��
��DH=2t����8��t��=3t��8��
�ߡ�HDI=��BAD=60�㣬
��tan��HDI= ![]() ��
��
��HI= ![]() DH��
DH��
��S=EFEG�� ![]() DHHI=2
DHHI=2 ![]() t2��
t2�� ![]() ��3t��8��2=��
��3t��8��2=�� ![]() t2+24
t2+24 ![]() t��32
t��32 ![]()

��4��4��3
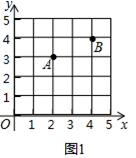
���������⣺��4����OO���ADʱ����ͼ2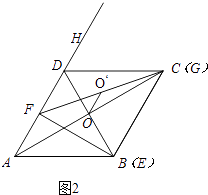
��ʱ��E��B�غϣ�
��t=4��
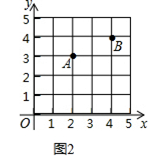
��OO���ADʱ����ͼ3��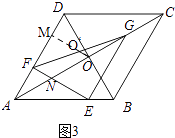
����O��OM��AD�ڵ�M��EF��OA�ཻ�ڵ�N��
�ɣ�2����֪��AF=t��AE=EG=2t��
��FN= ![]() t��
t��
��O���Ǿ���EFHG�ĶԽ��ߵĽ��㣬
��FM= ![]() EG=t��
EG=t��
��O��O��AD��O����FG���е㣬
��O��O�ǡ�FNG����λ�ߣ�
��O��O= ![]() FN=
FN= ![]() t��
t��
��AB=8��
���ɹ��ɶ�������ã�OA=4 ![]()
��OM=2 ![]() ��
��
��O��M=2 ![]() ��
�� ![]() t��
t��
��FE= ![]() t��EG=2t��
t��EG=2t��
���ɹ��ɶ�������ã�FG2=7t2 ��
���ɾ��ε����ʿ�֪��O��F2= ![]() FG2 ��
FG2 ��
���ɹ��ɶ�����֪��O��F2=O��M2+FM2 ��
�� ![]() t2=��2
t2=��2 ![]() ��
�� ![]() t��2+t2 ��
t��2+t2 ��
��t=3��t=��6����ȥ����
���Դ��ǣ�t=4��t=3��
�����㾫�����������ε����ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮