��Ŀ����
����Ŀ��ijУ�ٰ�һ��С�������ȣ���Ʒ�Ͻ�ʱ��Ϊ5��1����30�գ���ί���ͬѧ�ǽ�������Ʒ��ʱ��˳��ÿ5�����һ�飬��ÿһ��ļ�������ͳ�ƣ����Ƴ���ͼ��ʾ��ͳ��ͼ����֪�����Ҹ����εĸ߶ȱ�Ϊ2��3��4��6��4��1���������Ƶ����12�� 
����ش�
��1�����λ��������Ʒ������
��2������������ռ�ٷֱȻ��Ƴ�����ͳ��ͼ����ô�������Ӧ�����ε�Բ�Ľ����ȣ�
��3�����λ������2��һ�Ƚ���3�����Ƚ������Ƚ������㽱����������һ�����Ƚ���Ʒ���б�Ų������ɱ�����ȫһ�µĿ�Ƭ�����泯�ϵķ��ã����������ſ�Ƭ�����б�������״ͼ��鵽����Ʒǡ��һ����һ�Ƚ���һ���Ƕ��Ƚ��ĸ����Ƕ��٣�
���𰸡�
��1��60
��2��108
��3���⣺��һ�Ƚ���A��B��ʾ�����Ƚ���a��b��c��ʾ�����γ�ȡ��Ƭ�Ŀ��ܽ�����±���
A | B | a | b | c | |
A | ������ | ��B��A�� | ��a��A�� | ��b��A�� | ��c��A�� |
B | ��A��B�� | ������ | ��a��B�� | ��b��B�� | ��c��B�� |
a | ��A��a�� | ��B��a�� | ������ | ��b��a�� | ��c��a�� |
b | ��A��b�� | ��B��b�� | ��a��b�� | ������ | ��c��b�� |
c | ��A��c�� | ��B��c�� | ��a��c�� | ��b��c�� | ������ |
�ܹ���20�ֿ��ܽ����������12����һ��һ�Ƚ���һ�����Ƚ��Ŀ��������
�����������ſ�Ƭ���鵽����Ʒǡ��һ����һ�Ƚ���һ���Ƕ��Ƚ��ĸ���P=60%
���������⣺��1����������ã�12�� ![]() =60����������2����������ã�
=60����������2����������ã� ![]() ��360��=108�㣻 ���Դ��ǣ���1��60����2��108��
��360��=108�㣻 ���Դ��ǣ���1��60����2��108��
�����㾫����������Ҫ����������ͳ��ͼ������ͳ��ͼ�����֪ʶ�㣬��Ҫ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯���������ȷ�����⣮

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�����Ŀ��ijУ��������˲���ѧ�����͡�����ϲ����ͼ����𡱣�ֻѡһ���ѧ�������Ķ���������˵���ͳ�ƣ���������ͳ�ƺ���Ƴ�����ͳ�Ʊ�������ͳ��ͼ�������ͳ��ͼ���ṩ����Ϣ����������⣺
���� | Ƶ�� | Ƶ�� |
��ͨ�� | a |
|
ʱ����־ | b | 0.16 |
����С˵ | 50 | c |
��ѧ���� | d | e |
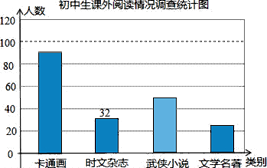
��1��������������______��ѧ����ͳ�Ʊ���a=______��d=______��
��2�������Դ�ͳ�Ʊ��������ͳ��ͼ��������С˵��Ӧ��Բ�Ľ���______��
��3���Թ��Ƹ�У1500��ѧ�����ж�����ͬѧ��ϲ����ѧ�������鼮��