��Ŀ����
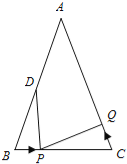
����Ŀ����ͼ����֪��ABC �У�AB=AC=6cm����B=��C��BC=4cm���� D Ϊ AB���е㣮
��1������� P ���߶� BC ���� 1cm/s ���ٶ��ɵ� B ��� C �˶���ͬʱ���� Q ���߶� CA ���ɵ� C ��� A �˶���
������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ����� 1 �����BPD ����CQP �Ƿ�ȫ�ȣ���˵�����ɣ�
������ Q ���˶��ٶ���� P ���˶��ٶȲ���ȣ����� Q ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD ����CQP ȫ�ȣ�
��2������ Q �Ԣ��е��˶��ٶȴӵ� C �������� P ��ԭ�����˶��ٶȴӵ� B ͬʱ����������ʱ���ء�ABC �����˶����� �� P ��� Q ��һ���ڡ�ABC �� �������������ں�����ֱ��д���𰸣�������д������̣�

���𰸡���1����ȫ�ȣ����ɼ�������1��5cm/s���ɼ�������2��24s����AC������
��������
���⣨1��������ʱ����ٶȷֱ����������������BP��CQ��BD��PC�ߵij�������SAS�ж�����������ȫ�ȣ�
������ȫ��������Ӧ���������̽���֮��Ĺ�ϵ���ٸ���·��=�ٶ���ʱ�乫ʽ������õ�P�˶���ʱ�䣬����õ�Q���˶��ٶȣ�
��2������������ͼ�η������֣����ڵ�Q���ٶȿ죬���ڵ�P��ǰ�ߣ�����Ҫ���һ����������Ӧ�ñȵ�P���ߵ��������ε������߳���
�⣺��1����ȫ�ȣ��������£�
��t=1�룬
��BP=CQ=1��1=1���ף�
��AB=6cm����DΪAB���е㣬
��BD=3cm��
����PC=BC��BP��BC=4cm��
��PC=4��1=3cm��
��PC=BD��
����AB=AC��
���B=��C��
���BPD�ա�CQP��
��������BPD�ա�CQP��
��vP��vQ��
��BP��CQ��
���ߡ�BPD�ա�CQP����B=��C����BP=CP=2��BD=CQ=3��
����P����Q�˶���ʱ��t=![]() =2�룬
=2�룬
��vQ=![]() ==1.5cm/s��
==1.5cm/s��
��2���辭��x����P���Q��һ��������
�����⣬�� 1.5x=x+2��6��
���x=24��
����P���˶���24s��1cm/s=24cm��
��24=2��12��
����P����Q��AC����������
������24���P���Q��һ���ڱ�AC��������