Question

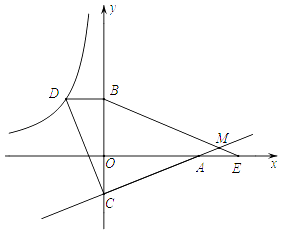
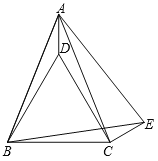
【题目】在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连结BD，CD，其中CD交直线AP与点E．

（1）如图1，若∠PAB＝30°，则∠ACE＝　 　；

（2）如图2，若60°＜∠PAB＜120°，请补全图形，判断由线段AB，CE，ED可以构成一个含有多少度角的三角形，并说明理由．

Answer 1

【答案】（1）30°；（2）线段AB，CE，ED可以构成一个含有60°角的三角形．

【解析】

（1）根据题意可得∠DAP＝∠BAP＝30°，然后根据AB＝AC，∠BAC＝60°，得出AD＝AC，∠DAC＝120°，最后根据三角形的内角和公式求解；

（2）由线段AB，CE，ED可以构成一个含有60度角的三角形，连接AD，EB，根据对称可得∠EDA＝∠EBA，然后证得AD＝AC，最后即可得出∠BAC＝∠BEC＝60°．

解：（1）连接AD，

∵点D与点B关于直线AP对称，

∴AD＝AB，∠DAP＝∠BAP＝30°，

∵AB＝AC，∠BAC＝60°，

∴AD＝AC，∠DAC＝120°，

∴2∠ACE+120°＝180°，

∴∠ACE＝30°，

故答案为：30°；

（2）线段AB，CE，ED可以构成一个含有60°角的三角形．

证明：连接AD，EB，如图2．

∵点D与点B关于直线AP对称，

∴AD＝AB，DE＝BE，

∴∠EDA＝∠EBA，

∵AB＝AC，AB＝AD，

∴AD＝AC，

∴∠ADE＝∠ACE，

∴∠ABE＝∠ACE．

设AC，BE交于点F，

又∵∠AFB＝∠CFE，

∴∠BAC＝∠BEC＝60°，

∴线段AB，CE，ED可以构成一个含有60°角的三角形．