题目内容
【题目】如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是 .
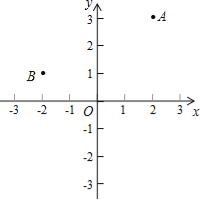
【答案】(﹣1,0).
【解析】
试题作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,求出C的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出k、b,得出直线BC的解析式,求出直线与x轴的交点坐标即可.
试题解析: 作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
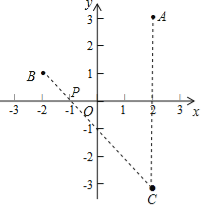
∵A点的坐标为(2,3),B点的坐标为(﹣2,1),
∴C(2,﹣3),
设直线BC的解析式是:y=kx+b,
把B、C的坐标代入得:![]()
解得![]() .
.
即直线BC的解析式是y=﹣x﹣1,
当y=0时,﹣x﹣﹣1=0,
解得:x=﹣1,
∴P点的坐标是(﹣1,0).

练习册系列答案
相关题目
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.