题目内容
【题目】如图,已知,在△ABC中,AB=AC,分别以AB、BC为边作等边△ABE和等边△BCD,连结CE、AD.
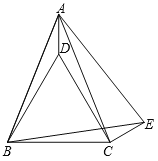
(1)求证:∠ACD=∠ABD;
(2)判断DC与CE的位置关系,并加以证明;
【答案】(1)见解析;(2)DC⊥CE,理由见解析
【解析】
(1)利用三角形全等进行证明.
(2)根据三角形全等求出△ABE为等边三角形,再利用条件得到△ABD≌△EBC即可解答.
(1)证明:∵△BCD为等边三角形,
∴DB=DC,
在△ABD与△ACD中,
∵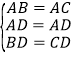
∴△ABD≌△ACD,
∴∠ABD=∠ACD
(2)解:DC⊥CE,证明如下:
由(1)可得△ABD≌△ACD,∴∠ADB=∠ADC,
又∵∠BDC=60°,
∴![]() ,
,
∵△ABE为等边三角形,
∴AB=BE,∠ABE=60°,
∴∠1=60°-∠3,
∵∠2=60°-∠3,
∴∠1=∠2,
在△ABD与△EBC中,
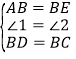
∴△ABD≌△EBC,
∴∠BCE=∠BDA=150°,
∴∠DCE=∠BCE-∠DCB=150°-60°= 90°.
∴DC⊥CE

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目