题目内容
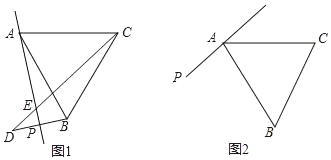
【题目】△ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP= . 
【答案】1或4
【解析】解:∵AB=AC=4,点D是边AB的中点,点E是边AC的中点,
∴BD=2,CE=2,∠B=∠C,
∵∠DPE=∠C,
∴∠BPD=180°﹣∠B﹣∠DPE,∠CEP=180°﹣∠EPC﹣∠C,
∴∠DPB=∠PEC,
∴△BPD∽△CPE,
∴ ![]() ,即
,即 ![]() ,
,
∴PB=1或4,
所以答案是:1或4.
【考点精析】通过灵活运用等腰三角形的性质和相似三角形的判定与性质,掌握等腰三角形的两个底角相等(简称:等边对等角);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目