��Ŀ����
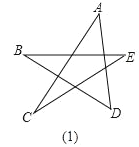
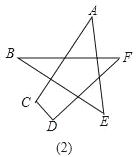
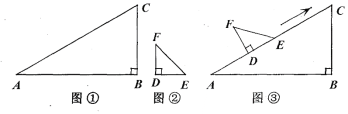
����Ŀ��ijͬѧ��һ�ο����У���ӲֽƬ��������ֱ�������Σ���ͼ�١��ڣ���ͼ���У���B=90������A=30����ͼ���У���D=90������F=45����ͼ���Ǹ�ͬѧ������һ��ʵ�飺������DEF��ֱ�DZ�DE����ABC��б��AC�غ���һ�𣬲�����DEF��AC�����ƶ������ƶ������У�D��E����ʼ����AC����(�ƶ���ʼʱ��D���A�غ�)��
(1)����DEF��AC�����ƶ��Ĺ����У���ͬѧ���֣�F��C�����ľ����� ������FC����FCE�Ķ����� �����������������������������С����
(2)��DEF���ƶ��Ĺ����У���FCE���CFE����֮���Ƿ�Ϊ��ֵ�������˵����
(3)�ܷ���DEF�ƶ���ijλ�ã�ʹF��C��������ABƽ�У����ܣ������CFE�Ķ����������ܣ���˵�����ɣ�
���𰸡���1����С�����2����ֵ����FCE+��CFE=��FED=45������3���ܣ���CFE=15����
��������
���⣨1������ͼ�εı仯�ó�F��C�����ľ���仯�ͣ���FCE�Ķ����仯���ɣ�
��2������ǵ����ʵó���FEC+��CFE=��FED=45�������ɵó��𰸣�
��3��ҪʹFC��AB��������FCE=��A=30���������ó���CFE�Ķ�����
�����������1��F��C�����ľ�����С������FC����FCE�Ķ�����ʴ�Ϊ����С�����
��2����FCE����CFE����֮��Ϊ��ֵ���������£�
�ߡ�D=90������DFE=45�������ߡ�D+��DFE+��FED=180�������FED=45�����ߡ�FED����FEC����ǣ����FEC+��CFE=��FED=45��������FCE����CFE����֮��Ϊ��ֵ��
��3��ҪʹFC��AB��������FCE=��A=30�������ߡ�CFE+��FCE=45�������CFE=45�㩁30��=15����

����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ�����������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
(���ۡ��ۼ۾����ֲ����������������룭�����ɱ�)
(1)��A��B�����ͺŵĵ���ȵ����۵��ۣ�
(2)���������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨����A���ͺŵĵ��������ܲɹ�����̨��
(3)��(2)����������������������30̨������ܷ�ʵ������Ϊ1400Ԫ��Ŀ�ꣿ�������������Ӧ�IJɹ�����������������˵�����ɣ�