题目内容
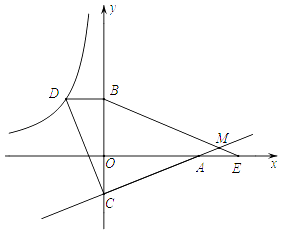
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
【答案】
(1)解:∵A(5,0),
∴OA=5.
∵ ![]() ,
,
∴ ![]() ,解得OC=2,
,解得OC=2,
∴C(0,﹣2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(﹣2,3),
∴m=﹣2×3=﹣6,
∴ ![]() ,
,
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,﹣2),
∴ ![]() ,解得
,解得  ,
,
∴ ![]() ;
;
(2)解:∵B(0,3),C(0,﹣2),
∴BC=5=OA,
在△OAC和△BCD中

∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)解:∠BMC=45°.
如图,连接AD,
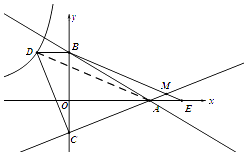
∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.
【解析】(1)由正切定义可求C坐标,进而由BD=OC求出D坐标,求出 反比例函数解析式;由A、C求出直线解析式;(2)由条件可判定△OAC≌△BCD,得出AC=CD,∠OAC=∠BCD,进而AC⊥CD;(3) 由已知可得AE=OC,BD=OC,得出AE=BD,再加平行得四边形AEBD为平行四边形,推出 △OAC≌△BCD,∴AC=CD,∵AC⊥CD,∴△ACD为等腰直角三角形,∴∠BMC=∠DAC=45°.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.