题目内容
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() 交边
交边![]() 于点
于点![]() .
.
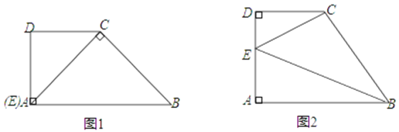
(1)当点![]() 与
与![]() 恰好重合时(如图1),求
恰好重合时(如图1),求![]() 的长;
的长;
(2)问:是否可能使![]() 、
、![]() 与
与![]() 都相似?若能,请求出此时
都相似?若能,请求出此时![]() 的长;若不能,请说明理由(如图2).
的长;若不能,请说明理由(如图2).
【答案】(1)2;(2)AD =2![]() .
.
【解析】
(1)由∠DCA=∠CAB,∠ADC=∠ACB,证得△ACD∽△ABC,利用相似三角形的对应边成比例,即可求得AD的长;
(2)分别从使△ABE、△CDE与△BCE都相似分析,利用相似三角形的性质,即可求得AD的长.
解:(1)当点E与A重合时,∵CD∥AB,
∴∠DCA=∠CAB,且∠ADC=∠ACB=90°,
∴△ACD∽△ABC,
∴![]() ,
,
∴AC=2![]() ,
,
∴AD=![]() .
.
(2)若能使△ABE、△CDE与△BCE都相似,
∴∠EBC=∠A=∠D=90°,∠DEC=∠BEC=∠AEB,
∵∠DEC+∠BEC+∠AEB=180,
∴∠DEC=∠BEC=∠AEB=60°.
在Rt△DEC中,tan∠DEC=![]() ,
,
∴DE=![]() .
.
在Rt△ABE中,tan∠AEB=![]() ,
,
∴EA=![]() ,
,
∴AD=DE+AE=2![]() .
.

练习册系列答案
相关题目
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
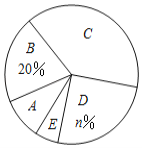
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.