题目内容
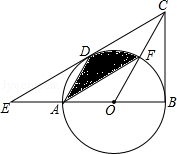
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

【答案】(1)见解析;(2)18°.
【解析】试题分析:(1)先由对角线互相平分证明四边形ABCD是平行四边形,再由对角互补得出∠ABC=90°,即可得出结论;
(2)先求出∠FDC=36°,再求出∠DCO=54°,然后求出∠ODC=54°,即可求出∠BDF.
试题解析:
(1)证明:∵AO=CO,BO=DO
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴OC=OD,
∴∠ODC=54°
∴∠BDF=∠ODC﹣∠FDC=18°.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目