Question

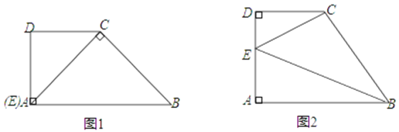
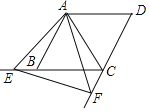
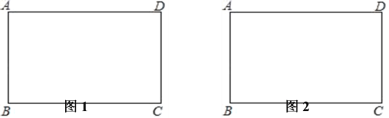
【题目】如图1，将矩形纸片ABCD(AD＞AB)沿BD折叠，点C落在点C′处.

(1)连接BD，请用直尺和圆规在图1中作出点C′；(不写作法，保留作图痕迹)

(2)若BC′与AD相交于点E，EB与ED的数量关系是　 　 ；连接AC′，则AC′与BD的位置关系是　 　；

(3)在(2)的条件下，若AB＝4，AD＝8，求BE的长．(提示：(2)、(3)两题可以在图2中作出草图完成)

Answer 1

【答案】(1)答案见解析；(2)相等，平行;（3）BE=5

【解析】

(1)过点C作BD的垂线垂足为H，以点H为圆心，CH为半径作弧画弧找到C′;

（2）通过证明△AEB△得出相应结果

（3）利用勾股定理建立方程求解即可

（1）如下图

（2）如下图

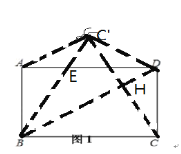
连接D

由折叠关系得到：D=CD=AB,∠BAC=∠B,

又∵∠AEB=∠

∴△AEB△（AAS）

∴EB=ED

（3）在ABE中

∴设，则

∴

∴

∴BE=5