题目内容
【题目】如图(1),![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() 点是底边
点是底边![]() 上的一个动点,
上的一个动点,![]() ,
,![]() .
.
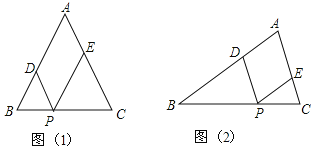
(1)用![]() 表示四边形
表示四边形![]() 的周长为 ;
的周长为 ;
(2)点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形,请说明理由;
是菱形,请说明理由;
(3)如果![]() 不是等腰三角形图(2),其他条件不变,点
不是等腰三角形图(2),其他条件不变,点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形(不必说明理由).
是菱形(不必说明理由).
【答案】(1)![]() ;(2)当
;(2)当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是菱形,见解析;(3)P运动到∠A的平分线上时,四边形ADPE是菱形,理由见解析.
是菱形,见解析;(3)P运动到∠A的平分线上时,四边形ADPE是菱形,理由见解析.
【解析】
(1)根据平行线的性质和等腰三角形的性质证明∠B=∠DPB,∠C=∠EPC,进而可得DB=DP,PE=EC,从而可得四边形ADPE的周长=AD+DP+PE+AE=AB+AC;
(2)当P运动到BC中点时,四边形ADPE是菱形;首先证明四边形ADPE是平行四边形,再证明DP=PE即可得到四边形ADPE是菱形;
(3)P运动到∠A的平分线上时,四边形ADPE是菱形,首先证明四边形ADPE是平行四边形,再根据平行线的性质可得∠1=∠3,从而可证出∠2=∠3,进而可得AE=EP,然后可得四边形ADPE是菱形.
(1)∵PD∥AC,PE∥AB,
∴∠DPB=∠C,∠EPC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠DPB,∠C=∠EPC,
∴DB=DP,PE=EC,
∴四边形ADPE的周长是:AD+DP+PE+AE=AB+AC=2a;
(2)当P运动到BC中点时,四边形ADPE是菱形;
∵PD∥AC,PE∥AB,
∴四边形ADPE是平行四边形,
∴PD=AE,PE=AD,
∵PD∥AC,PE∥AB,
∴∠DPB=∠C,∠EPC=∠B,
∵P是BC中点,
∴PB=PC,
在△DBP和△EPC中,
 ,
,
∴△DBP≌△EPC(ASA),
∴DP=EC,
∵EC=PE,
∴DP=EP,
∴四边形ADPE是菱形;
(3)P运动到∠A的平分线上时,四边形ADPE是菱形,
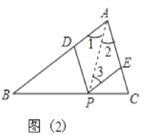
∵PD∥AC,PE∥AB,
∴四边形ADPE是平行四边形,
∵AP平分∠BAC,
∴∠1=∠2,
∵AB∥EP,
∴∠1=∠3,
∴∠2=∠3,
∴AE=EP,
∴四边形ADPE是菱形.

【题目】全民健身运动已成为一种时尚 ,为了解揭阳市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷内容包括五个项目:
A:健身房运动;B:跳广场舞;C:参加暴走团;D:散步;E:不运动.
以下是根据调查结果绘制的统计图表的一部分,
运动形式 | A | B | C | D | E |
人数 |
|
|
|
|
|
请你根据以上信息,回答下列问题:
![]() 接受问卷调查的共有 人,图表中的
接受问卷调查的共有 人,图表中的![]() ,
,![]() .
.
![]() 统计图中,
统计图中,![]() 类所对应的扇形的圆心角的度数是 度.
类所对应的扇形的圆心角的度数是 度.

![]() 揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有
揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有![]() 人,请你估计一下该社区参加环岛路“暴走团”的人数.
人,请你估计一下该社区参加环岛路“暴走团”的人数.
【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7