题目内容
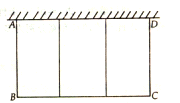
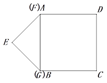
【题目】如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG
以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止
运动.设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大
致图象为( )
A. 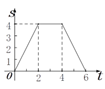 B.
B. 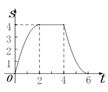 C.
C. 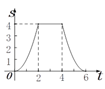 D.
D. 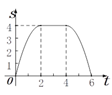
【答案】B
【解析】分析:根据题意可以求出各段对应的函数图象,从而可以判断哪个选项中的函数图象符合要求,本题得以解决.
详解:由题意可得,
FE=GE,AB=FG=4,∠FEG=90°,
则FE=GE=2![]() ,点E到FG的距离为2,
,点E到FG的距离为2,
当点E从开始到点E到边BC上的过程中,
S=![]() (0≤t≤2),
(0≤t≤2),
当点E从BC边上到边FG与DC重合时,S=![]() =4(2≤t≤4),
=4(2≤t≤4),
当边FG与DC重合到点E到边DC的过程中,
S=![]() =(6-t)2(4≤t≤6),
=(6-t)2(4≤t≤6),
由上可得,选项B中函数图象符合要求,
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目