题目内容
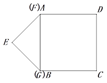
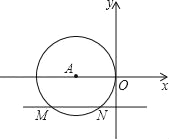
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为_____.
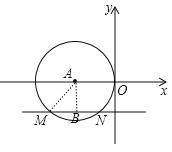
【答案】(﹣2,﹣4)
【解析】分析:作AB⊥MN于B,连结AM,如图,设⊙A的半径为r,先根据切线的性质得OA=r,则点A的坐标为(﹣r,0),再利用垂径定理得BM=BN,利用MN∥x轴,M(﹣8,﹣4),得到B点坐标为(﹣r,﹣4),然后在Rt△ABM中,根据勾股定理得42+(8﹣r)2=r2,解得r=5,则BM=BN=3,易得N点坐标为(﹣2,﹣4).
详解:作AB⊥MN于B,连结AM,如图,设⊙A的半径为r.
∵⊙A与y轴相切于原点O,∴OA=r,∴点A的坐标为(﹣r,0).
∵AB⊥MN,∴BM=BN.
∵MN∥x轴,M(﹣8,﹣4),∴B点坐标为(﹣r,﹣4).在Rt△ABM中,AB=4,AM=r,BM=8﹣r.
∵AB2+BM2=AM2,∴42+(8﹣r)2=r2,解得:r=5,∴BM=3,∴BN=3,∴N点坐标为(﹣2,﹣4).
故答案为:(﹣2,﹣4).

练习册系列答案
相关题目