题目内容
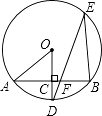
【题目】如图,点E是正方形ABCD的边BC延长线上的一点,AC=CE,AE交CD于点F,则∠AFD的度数是 . 
【答案】67.5°
【解析】解:∵CE=AC, ∴∠E=∠CAE,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴∠E+∠CAE=45°,
∴∠E= ![]() ×45°=22.5°,
×45°=22.5°,
在△CEF中,∠AFD=∠ECF=90°﹣22.5°=67.5°
所以答案是:67.5°.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目