题目内容
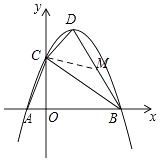
【题目】如图,在平面直角坐标系中xOy中,抛物线y=﹣x2+bx+c与x轴相交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D,联结AC,BC,DB,DC. 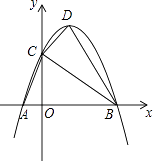
(1)求这条抛物线的表达式及顶点D的坐标;
(2)求证:△ACO∽△DBC;
(3)如果点E在x轴上,且在点B的右侧,∠BCE=∠ACO,求点E的坐标.
【答案】
(1)解:∵抛物线y=﹣x2+bx+c经过点A(﹣1,0),点C(0,3),
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线的表达式为y=﹣x2+2x+3,
∴顶点D的坐标为(1,4)
(2)解:∵当y=0时,0=﹣x2+2x+3,
解得x1=﹣1,x2=3,
∴B(3,0),
又∵A(﹣1,0),D(1,4),
∴CD= ![]() ,BC=3
,BC=3 ![]() ,BD=2
,BD=2 ![]() ,AO=1,CO=3,
,AO=1,CO=3,
∴CD2+BC2=BD2,
∴△BCD是直角三角形,且∠BCD=90°,
∴∠AOC=∠DCB,
又∵ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴△ACO∽△DBC
(3)解:设CE与BD交于点M,
∵△ACO∽△DBC,
∴∠DBC=∠ACO,
又∵∠BCE=∠ACO,
∴∠DBC=∠BCE,
∴MC=MB,
∵△BCD是直角三角形,
∴∠BCM+∠DCM=90°=∠CBM+∠MDC,
∴∠DCM=∠CDM,
∴MC=MD,
∴DM=BM,即M是BD的中点,
∵B(3,0),D(1,4),
∴M(2,2),
设直线CE的解析式为y=kx+b,则
![]() ,
,
解得 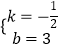 ,
,
∴直线CE为:y=﹣ ![]() x+3,
x+3,
当y=0时,0=﹣ ![]() x+3,
x+3,
解得x=6,
∴点E的坐标为(6,0).
【解析】(1)根据抛物线y=﹣x2+bx+c经过点A(﹣1,0),点C(0,3),即可求得b,c的值,进而得到抛物线的表达式及顶点D的坐标;(2)先根据B(3,0),A(﹣1,0),D(1,4),求得CD= ![]() ,BC=3
,BC=3 ![]() ,BD=2
,BD=2 ![]() ,AO=1,CO=3,进而得到CD2+BC2=BD2 , 从而判定△BCD是直角三角形,且∠BCD=90°,最后根据∠AOC=∠DCB,
,AO=1,CO=3,进而得到CD2+BC2=BD2 , 从而判定△BCD是直角三角形,且∠BCD=90°,最后根据∠AOC=∠DCB, ![]() =
= ![]() ,判定△ACO∽△DBC;(3)先设CE与BD交于点M,根据MC=MB,得出M是BD的中点,再根据B(3,0),D(1,4),得到M(2,2),最后根据待定系数法求得直线CE的解析式,即可得到点E的坐标.
,判定△ACO∽△DBC;(3)先设CE与BD交于点M,根据MC=MB,得出M是BD的中点,再根据B(3,0),D(1,4),得到M(2,2),最后根据待定系数法求得直线CE的解析式,即可得到点E的坐标.
【考点精析】认真审题,首先需要了解勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形),还要掌握相似三角形的判定(相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS))的相关知识才是答题的关键.