题目内容
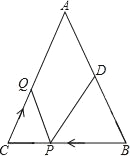
【题目】如图,已知AE平分∠BAC,点D是AE上一点,连接BD,CD.请你添加一个适当的条件,使△ABD≌△ACD.添加的条件是:____.(写出一个即可)

【答案】AB=AC或∠B=∠C或∠BDA=∠CDA或∠BDE=∠CDE(四者选一即可)
【解析】
先找到证△ABD≌△ACD的已知条件,然后再根据全等三角形的判定定理添加条件即可.
解:∵AE平分∠BAC,
∴∠BAD=∠CAD
∵AD=AD
再添加AB=AC,可用SAS证明△ABD≌△ACD;
再添加∠B=∠C,可用AAS证明△ABD≌△ACD;
再添加∠BDA=∠CDA,可用ASA证明△ABD≌△ACD;
再添加∠BDE=∠CDE,根据等角的补角相等,可得:∠BDA=∠CDA,可用ASA证明△ABD≌△ACD;
故答案为:AB=AC或∠B=∠C或∠BDA=∠CDA或∠BDE=∠CDE(四者选一即可)

练习册系列答案
相关题目
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚