题目内容
【题目】如图,已知△ABC中,AB=AC,AD为中线,点P是AD上一点,点Q是AC上一点,且∠BPQ+∠BAQ=180°.
(1)若∠ABP=α,求∠PQC的度数(用含α的式子表示);
(2)求证:BP=PQ.

【答案】(1)α;(2)见解析.
【解析】
(1)由四边形的内角和即可求出∠AQP,从而求出∠PQC;
(2)过点P分别作PE⊥AB于E,PF⊥AC于F,证明△PEB≌△PFQ即可.
解:(1)∵∠BPQ+∠BAQ=180°,∠ABP=α
∴∠AQP=360°-∠BPQ-∠BAQ-∠ABP=180°-α
∴∠PQC=180°-∠AQP=α
(2)过点P分别作PE⊥AB于E,PF⊥AC于F
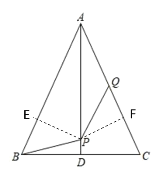
∵AB=AC,AD为△ABC的中线
∴AD平分∠BAC
∴PE=PF
在△PEB和△PFQ中

∴△PEB≌△PFQ
∴BP=PQ

练习册系列答案
相关题目