题目内容
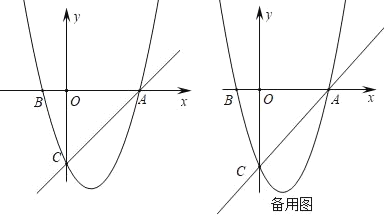
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)求抛物线的解析式;
(2)若动点P在第四象限内的抛物线上,过动点P作x轴的垂线交直线AC于点D,交x轴于点E,垂足为E,求线段PD的长,当线段PD最长时,求出点P的坐标;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)![]() ;(3)存在,点P的坐标为(1,﹣4)或(﹣2,5).
;(3)存在,点P的坐标为(1,﹣4)或(﹣2,5).
【解析】
(1)将点A、C的坐标代入函数表达式得:即可求解;
(2)设点P(x,x2-2x-3),则点D(x,x-3),则PD=x-3-(x2-2x-3)=-x2+3x,即可求解;
(3)分∠ACP=90°、∠P′AC=90°两种情况,分别求解.
(1)将点A、C的坐标代入函数表达式得:![]() ,解得:
,解得:![]() ,
,
故:函数的表达式为:y=x2﹣2x﹣3…①;
(2)设直线AC的表达式为:y=kx+b,则:![]() ,
,
故直线BC的表达式为:y=x﹣3,
设点P(x,x2﹣2x﹣3),则点D(x,x﹣3),
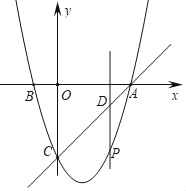
∴PD=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∵﹣1<0,抛物线开口向下,当x=![]() 时,PD的最大值为
时,PD的最大值为![]() ,
,
此时,点P(![]() ,﹣
,﹣![]() );
);
(3)存在,理由:
①当∠ACP=90°时,
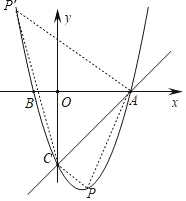
由(2)知,直线AC的表达式为:y=x﹣3,
故直线CP的表达式为:y=﹣x﹣3…②,
①②联立并解得:x=1或0(舍去x=0),
故点P坐标为(1,﹣4);
②当∠P′AC=90°时,
设直线AP′的表达式为:y=﹣x+b,
将x=3,y=0代入并解得:b=3,
故:直线AP′的表达式为:y=﹣x+3…③,
联立①③并解得:x=﹣2或3(舍去x=3),
故:点P′的坐标为(﹣2,5);
故点P的坐标为(1,﹣4)或(﹣2,5).

 阅读快车系列答案
阅读快车系列答案